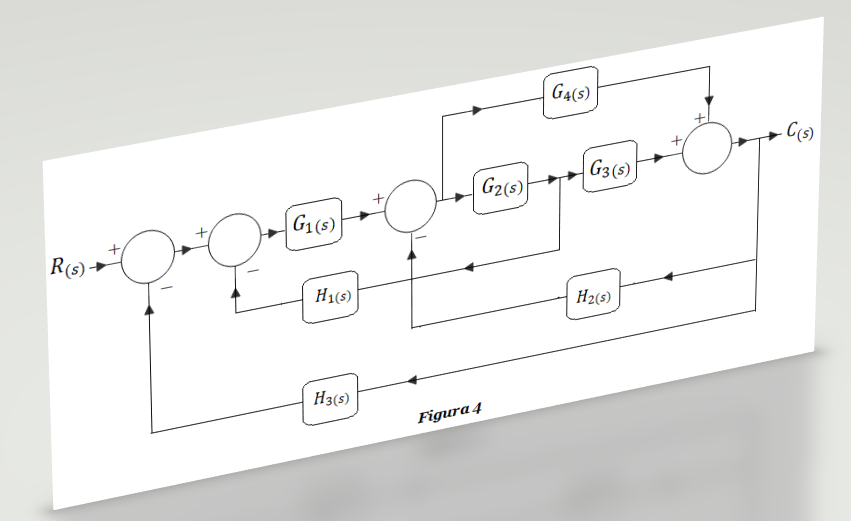
Un Diagrama de Bloques es una de las herramientas más poderosas para el análisis de señales y sistemas. En el Diagrama de Bloques de la Figura 4 cada bloque representa en sí mismo la Función de Transferencia de un subsistema. El aporte más importante de un diagrama de bloques es que permite al ingeniero de control visualizar la operación y funcionalidad del sistema en su totalidad, de una manera incluso más práctica que observando directamente el sistema físico mismo.
En los siguientes ejercicios de diagramas de bloques se determina la Función de Transferencia de sistemas aplicando álgebra de bloques. Estos ejercicios que forman parte rutinaria de materias como sistemas de control, señales y sistemas, sistemas electromecánicos y mecatrónicos, etc. El método para hallar la solución se corresponde con las mejores prácticas estudiadas en los textos tradicionales de Sistemas de Control.
Ejercicios resueltos de Diagramas de Bloques
El objetivo al aplicar el álgebra de bloques para la reducción de diagramas de bloques es hacer que los bucles estén anidados unos dentro de otros o que los bucles estén completamente separados para que se pueda aplicar la regla 8 de la tabla de equivalencias. Hay que tener en cuenta que no se puede cambiar un punto de suma con un punto de bifurcación ni viceversa.
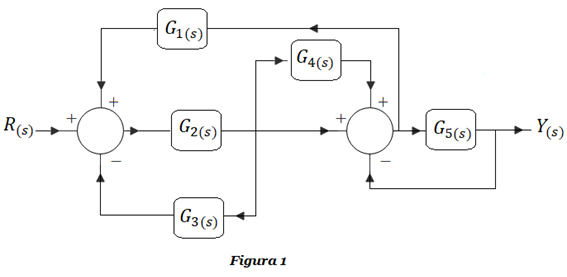
Ejercicio DB-1: Obtener la función de transferencia G(s)=Y(s)/R(s) de la Figura 1, empleando técnicas de reducción por álgebra de bloques. Encontrar la misma solución con la fórmula de Mason.
Encontrarás la solución al ejercicio DB-1 en el siguiente link: SOLUCIÓN Ejercicio DB-1.
Fórmula de Mason – Ejercicio resuelto 1.
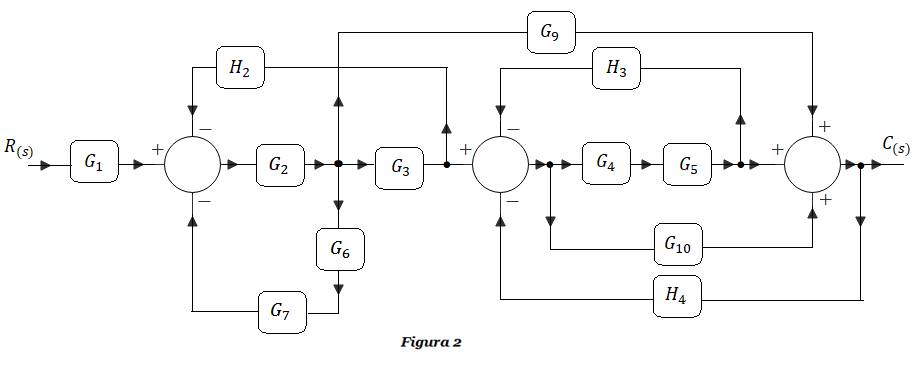
Ejercicio DB-2: Obtener la función de transferencia G(s)=C(s)/R(s) de la Figura 2, empleando técnicas de reducción por álgebra de bloques.
Encontrarás la solución al ejercicio DB-2 en el siguiente link: SOLUCIÓN Ejercicio DB-2.
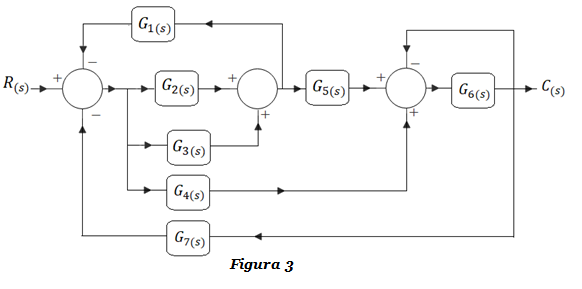
Ejercicio DB-3: Obtener la función de transferencia G(s)=C(s)/R(s) de la Figura 3, empleando técnicas de reducción por álgebra de bloques. Encontrar la misma solución con la fórmula de Mason.
Encontrarás la solución al ejercicio DB-3 en el siguiente link: SOLUCIÓN Ejercicio DB-3.
Fórmula de Mason – Ejercicio resuelto 2.
Ejercicio DB-4: Obtener la función de transferencia G(s)=C(s)/R(s) de la Figura 4, empleando técnicas de reducción por álgebra de bloques.
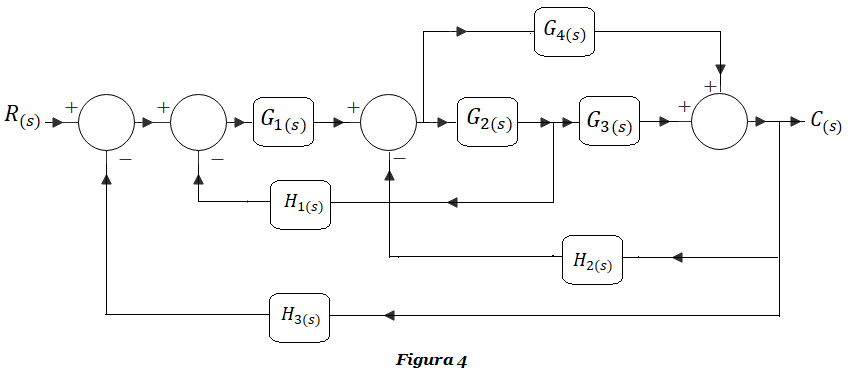
Encontrarás la solución al ejercicio DB-4 en el siguiente link: SOLUCIÓN Ejercicio DB-4.
Ejercicio FT-7: Obtener el diagrama de bloques del sistema y luego utilizar álgebra de bloques para Obtener la Función de Transferencia H2(s)=Y2(s)/U(s) del sistema masa-resorte-amortiguador de la Figura 67, a partir del diagrama de bloques obtenido.
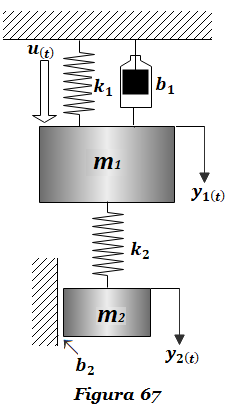
Encontrarás la solución al ejercicio FT-7 en el siguiente link: SOLUCIÓN Ejercicio FT-7.
Te puede interesar:
- Se resuelven ejercicios de Determinar la Función de Transferencia, resolver Diagramas de Bloques, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…
Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos. Al suscribirte podrás contar con excelente material para estudiar y superar con éxito las demandas académicas.
Curso relacionado:
Artículos relacionados:
- Función de Transferencia – Teoría.
- Sistemas de Primer Orden – Teoría.
- Linealidad e Invariancia en el tiempo – Teoría (memoria, estabilidad y causalidad).
- Señales Básicas – Introducción.
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs
