El Error en Estado Estable (o régimen permanente) es uno de los objetivos más comunes de un sistema de control. Este objetivo consiste en lograr que la señal de salida del sistema en estado estable siga de manera automática y exacta a una señal de referencia presente en la entrada del sistema. Este objetivo es difícil de obtener en un 100%, por lo que un diseño razonable busca minimizar al máximo el Error del Sistema en Estado Estable mientras se satisfacen ciertos requerimientos y especificaciones en la Respuesta Transitoria del sistema. La Figura adjunta muestra varios niveles de error ante una entrada escalón unitario para un sistema de control cuya Función de Transferencia de trayectoria directa es un sistema de primer orden.
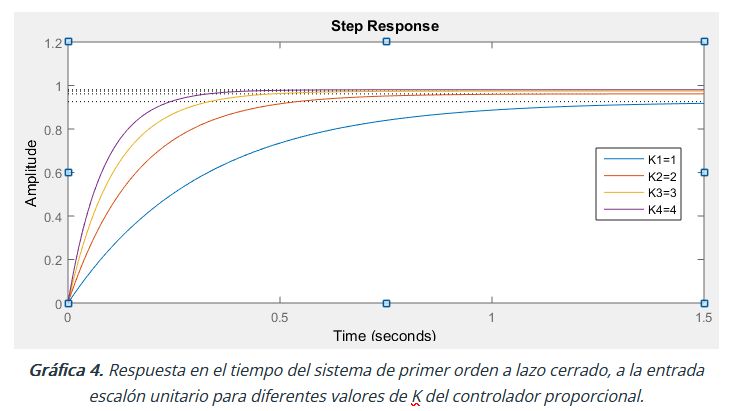
Error en Estado Estable – Definición
Supongamos que la señal y(t) es la salida de un sistema de control cualquiera. Uno de los objetivos más comunes de un sistema de control es que su señal de salida en estado estable siga de manera automática y exacta a una señal de referencia presente en la entrada del sistema. La señal de error e(t) de un sistema de control en todo tiempo t se puede definir como la diferencia entre la salida y(t) del sistema y la señal de referencia:
\boldsymbol e(\boldsymbol t) = \boldsymbol s\boldsymbol e\boldsymbol ñ\boldsymbol a\boldsymbol l\ \boldsymbol d\boldsymbol e\ \boldsymbol r\boldsymbol e\boldsymbol f\boldsymbol e\boldsymbol r\boldsymbol e\boldsymbol n\boldsymbol c\boldsymbol i\boldsymbol a - \boldsymbol y(\boldsymbol t)
La ecuación anterior implica un sistema de realimentación donde las señales que se restan (que se comparan) deben tener las mismas unidades. Esto último por lo general se logra colocando un sensor en la rama de realimentación con una ganancia que conceda a ambas señales el mismo nivel de valores. Este ajuste de los rangos de señal a los rangos de la entrada equivale a multiplicar la señal de salida por la ganancia estática de la realimentación.
Luego:
El Error en Estado Estable ess de un sistema de control se define como:
\boldsymbol e_{\boldsymbol s\boldsymbol s} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol t\rightarrow \mathbf \infty}\boldsymbol e(\boldsymbol t)Para contar con una expresión más práctica al calcular el error en estado estable de un sistema de control, nos apoyamos en el “Teorema dela valor final” visto en Transformada de Laplace:
\boldsymbol e_{\boldsymbol s\boldsymbol s} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol t\rightarrow \mathbf \infty}\boldsymbol e(\boldsymbol t) = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\mathbf s\rightarrow 0}sE(\boldsymbol s)\ \ \ \ (1)La ecuación (1) nos muestra que necesitamos la Transformada de Laplace de la señal de error e(t). Considere el sistema de la Figura 1:
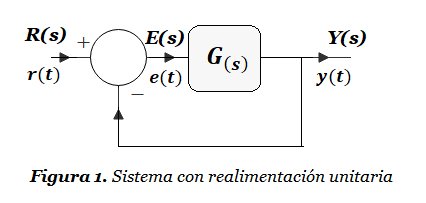
En el caso del sistema de control con realimentación unitaria de la Figura 1, la señal de referencia es directamente r(t). Por lo tanto, El error e(t) es:
\boldsymbol e(\boldsymbol t) = \boldsymbol r(t) - \boldsymbol y(\boldsymbol t)\ \ \ \ (2)
Con el fin de obtener una función de transferencia entre el error del sistema y la señal de referencia, dividimos ambos lados de la ecuación (2) entre r(t):
\frac{e(t)}{r(t)} = \frac{r(t) - y(t)}{r(t)} = 1 - \frac{y(t)}{r(t)}\ \ \ \ (3)Obtenemos la Transformada de Laplace de (3):
\frac{E(s)}{R(s)} = 1 - \frac{Y(s)}{R(s)}\ \ \ \ (4)En (4) identificamos un cociente que podemos obtener al aplicar álgebra de bloques (ver ) al diagrama de la Figura 1:
\frac{Y(s)}{R(s)} = \frac{G(s)}{1 + G(s)}\ \ \ \ (5)Sustituimos (5) en (4):
\frac{E(s)}{R(s)} = 1 - \frac{G(s)}{1 + G(s)} = \frac{1 + G(s) - G(s)}{1 + G(s)} = \frac{1}{1 + G(s)}\ \ \ \ (6)Despejamos E(s) en (6):
E(s) = \left(\frac{1}{1 + G(s)}\right)R(s)\ \ \ \ (7)Sustituimos (7) en (1):
\boldsymbol e_{\boldsymbol s\boldsymbol s} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\mathbf s\rightarrow 0}sE(\boldsymbol s)= \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\mathbf s\rightarrow 0}s\left(\frac{1}{1 + \boldsymbol G\left(\boldsymbol s\right)}\right)\boldsymbol R\left(\boldsymbol s\right)\ \ \ \ (8)En la ecuación (8) se nota claramente que ess depende de las características de la función de transferencia de trayectoria directa G(s). Más específicamente, ess dependerá del número de polos que G(s) tenga en el origen (en s=0). Este número de polos se conoce como el Tipo de un sistema de control.
Tipos de Sistema de Control
En general, la función de transferencia de trayectoria directa G(s) de la Figura 1 se puede expresar como:
\boldsymbol G\left(\boldsymbol s\right) = \boldsymbol K\frac{(\boldsymbol T_{\boldsymbol a}\boldsymbol s + 1)(\boldsymbol T_{\boldsymbol b}\boldsymbol s + 1)\ldotp \ldotp \ldotp (\boldsymbol T_{\boldsymbol m}\boldsymbol s + 1)}{\boldsymbol s^{\boldsymbol N}(\boldsymbol T_1\boldsymbol s + 1)(\boldsymbol T_2\boldsymbol s + 1)\ldotp \ldotp \ldotp (\boldsymbol T_{\boldsymbol p}\boldsymbol s + 1)}\ \ \ \ (9)En (9) el término sN representa un polo de multiplicidad N. Un sistema de control se denomina de Tipo 0, 1, 2,…si N=0, 1, 2… respectivamente. Conforme el número de Tipo de sistema es mayor aumenta la precisión, pero disminuye la estabilidad. En la práctica es muy raro tener sistemas Tipo 3 o más pues colocar 3 o más integradores en la trayectoria directa afectan negativamente la estabilidad del sistema.
La ecuación (8) nos permite obtener el error en estado estable para diferentes entradas de prueba. Al estudiar estos casos veremos que la K de la ecuación (9) está directamente relacionada con el error en estado estable.
Señales de prueba para evaluar el error en estado estable.
El error en estado estable para un sistema de control es la diferencia entre la entrada y la salida para una entrada de prueba específica. Las entradas de prueba utilizadas para el análisis y diseño de errores de estado estable se resumen a continuación.
El escalón unitario, u(t):
Las entradas de escalón unitario representan una posición constante y, por lo tanto, son útiles para determinar la capacidad del sistema de control para posicionarse con respecto a un objetivo estacionario.
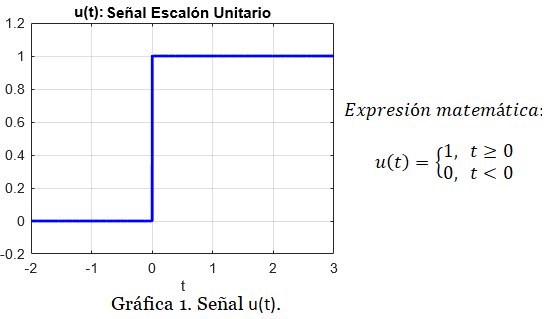
La rampa unitaria, r(t):
Las entradas de rampa representan entradas de velocidad constante a un sistema de control de posición, con una amplitud que aumenta linealmente. Estas formas de onda se pueden utilizar para probar la capacidad de un sistema para seguir una entrada (una posición) que aumenta linealmente o, de manera equivalente, para rastrear un objetivo de velocidad constante.
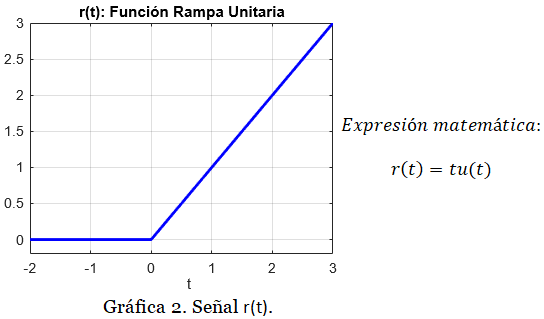
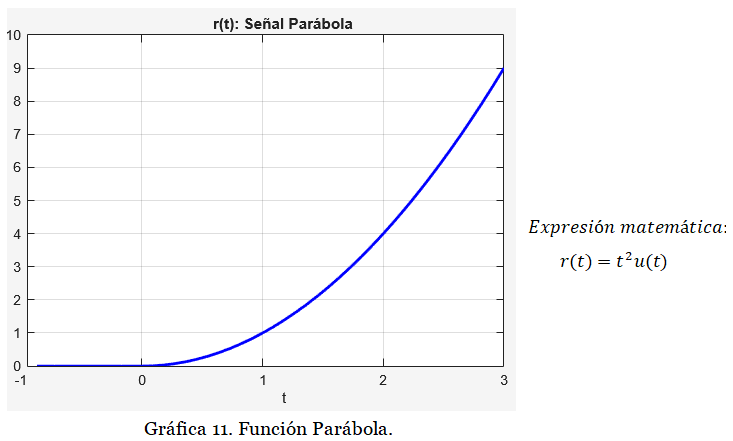
La parábola r(t):
Las entradas parabólicas, cuyas segundas derivadas son constantes, representan entradas de aceleración constantes para los sistemas de control de posición y se pueden usar para representar objetivos acelerados.
Sustituiremos ahora diferentes tipos de entrada en la ecuación (8) y obtendremos relaciones importantes entre la función de transferencia de trayectoria directa G(s) y el Error en Estado Estable ess .
Error en estado estable ante entrada Escalón Unitario.
Utilizamos la ecuación (8). Cuando la entrada al sistema de control es la función escalón unitario, calculamos el error en estado estable de la manera siguiente:
r(t) = u(t)\ \mathop{\leftrightarrow}\limits^{{\mathcal{L}}}\ R(s) = \frac{1}{s}e_{ss} = \lim_{s\rightarrow 0}s\left(\frac{1}{1 + G(s)}\right)\left(\frac{1}{s}\right) = \lim_{s\rightarrow 0}\left(\frac{1}{1 + G(s)}\right)\Rightarrow \Rightarrow \boldsymbol e_{\boldsymbol s\boldsymbol s} = \frac{1}{1 + \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\boldsymbol G(\boldsymbol s)}Por conveniencia práctica hacemos la siguiente definición:
Se denomina Constante de Error Escalón, Kp , (o constante de posición, «position constant» ) a la siguiente expresión:
\boldsymbol K_{\boldsymbol p} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\boldsymbol G\left(\boldsymbol s\right)\ \ \ \ (10)Por lo tanto:
El Error en Estado Estable de un sistema de control ante una entrada escalón unitario, ess (step) , es:
\boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol s\boldsymbol t\boldsymbol e\boldsymbol p) = \frac{1}{1 + \boldsymbol K_{\boldsymbol p}}\ \ \ \ (11)Decíamos antes que ess (step) dependerá del número de polos que G(s) tenga en el origen (en s=0). Mediante el siguiente análisis, utilizando las ecuaciones (9), (10) y (11) podremos ver esta dependencia.También decíamos que la K de la ecuación (9) está directamente relacionada con el error en estado estable:
Sistema\ tipo\ cero\Rightarrow N=0\Rightarrow \boldsymbol G\left(\boldsymbol s\right) = \boldsymbol K\frac{(\boldsymbol T_{\boldsymbol a}\boldsymbol s + 1)(\boldsymbol T_{\boldsymbol b}\boldsymbol s + 1)\ldotp \ldotp \ldotp (\boldsymbol T_{\boldsymbol m}\boldsymbol s + 1)}{(\boldsymbol T_1\boldsymbol s + 1)(\boldsymbol T_2\boldsymbol s + 1)\ldotp \ldotp \ldotp (\boldsymbol T_{\boldsymbol p}\boldsymbol s + 1)}\Rightarrow\Rightarrow\boldsymbol K_{\boldsymbol p} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\boldsymbol G\left(\boldsymbol s\right)=\boldsymbol K \Rightarrow\boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol s\boldsymbol t\boldsymbol e\boldsymbol p) = \frac{1}{1 + \boldsymbol K}=\boldsymbol constanteSistema\ tipo\ uno \ o\ mayor\Rightarrow N=1, 2,3...\Rightarrow\boldsymbol G\left(\boldsymbol s\right) = \boldsymbol K\frac{(\boldsymbol T_{\boldsymbol a}\boldsymbol s + 1)(\boldsymbol T_{\boldsymbol b}\boldsymbol s + 1)\ldotp \ldotp \ldotp (\boldsymbol T_{\boldsymbol m}\boldsymbol s + 1)}{\boldsymbol s^{\boldsymbol N}(\boldsymbol T_1\boldsymbol s + 1)(\boldsymbol T_2\boldsymbol s + 1)\ldotp \ldotp \ldotp (\boldsymbol T_{\boldsymbol p}\boldsymbol s + 1)}\Rightarrow\Rightarrow\boldsymbol K_{\boldsymbol p} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\boldsymbol G\left(\boldsymbol s\right)=\boldsymbol \infty \Rightarrow\boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol s\boldsymbol t\boldsymbol e\boldsymbol p) = \frac{1}{1 + \boldsymbol \infty }=\boldsymbol 0Resumiendo:
El Error en Estado Estable de un sistema de control ante una entrada escalón unitario, ess (step) , es:
\bigtriangleup \boldsymbol S\boldsymbol i\boldsymbol s\boldsymbol t\boldsymbol e\boldsymbol m\boldsymbol a\ \boldsymbol T\boldsymbol i\boldsymbol p\boldsymbol o\ 0\Rightarrow \boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol s\boldsymbol t\boldsymbol e\boldsymbol p) = \frac{1}{1 + \boldsymbol K_{\boldsymbol p}}; \ \ \ \ \boldsymbol K_{\boldsymbol p} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\boldsymbol G\left(\boldsymbol s\right) \bigtriangleup \boldsymbol S\boldsymbol i\boldsymbol s\boldsymbol t\boldsymbol e\boldsymbol m\boldsymbol a\ \boldsymbol T\boldsymbol i\boldsymbol p\boldsymbol o\ 1\ o\ mayor\Rightarrow \boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol s\boldsymbol t\boldsymbol e\boldsymbol p) = 0G(s) : Función de transferencia de trayectoria directa.
Error en estado estable ante una entrada Rampa.
Repitiendo el procedimiento del apartado anterior, cuando la entrada al sistema de control es la función rampa de pendiente uno, calculamos el error en estado estable de la manera siguiente:
r(t) = tu(t)\ \mathop{\leftrightarrow}\limits^{{\mathcal{L}}}\ R(s) = \frac{1}{s^2}e_{ss} = \lim_{s\rightarrow 0}s\left(\frac{1}{1 + G(s)}\right)\left(\frac{1}{s^2}\right) = \lim_{s\rightarrow 0}\left(\frac{1}{1 + G(s)}\right)\left(\frac{1}{s}\right)\Rightarrow \Rightarrow \boldsymbol e_{\boldsymbol s\boldsymbol s} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\frac{1}{\boldsymbol s + \boldsymbol s\boldsymbol G(\boldsymbol s)}= \frac{1}{ \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\boldsymbol s\boldsymbol G(\boldsymbol s)}Se denomina Constante de Error Rampa, Kv , (o constante de velocidad, «velocity constant» ) a la siguiente expresión:
\boldsymbol K_{\boldsymbol v} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\boldsymbol s\boldsymbol G\left(\boldsymbol s\right)Por lo tanto:
El Error en Estado Estable de un sistema de control ante una entrada rampa unitaria, ess (ramp) , es:
\boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol r\boldsymbol a\boldsymbol m\boldsymbol p) = \frac{1}{\boldsymbol K_{\boldsymbol v}}Sistema\ tipo\ cero\Rightarrow N=0\Rightarrow \boldsymbol K_{\boldsymbol v} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\boldsymbol s\boldsymbol G\left(\boldsymbol s\right)=\boldsymbol 0 \Rightarrow\boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol r\boldsymbol a\boldsymbol m\boldsymbol p) = \frac{1}{\boldsymbol 0}=\mathbf \infty Sistema\ tipo\ uno \Rightarrow N=1\Rightarrow\boldsymbol G\left(\boldsymbol s\right) = \boldsymbol K\frac{(\boldsymbol T_{\boldsymbol a}\boldsymbol s + 1)(\boldsymbol T_{\boldsymbol b}\boldsymbol s + 1)\ldotp \ldotp \ldotp (\boldsymbol T_{\boldsymbol m}\boldsymbol s + 1)}{\boldsymbol s(\boldsymbol T_1\boldsymbol s + 1)(\boldsymbol T_2\boldsymbol s + 1)\ldotp \ldotp \ldotp (\boldsymbol T_{\boldsymbol p}\boldsymbol s + 1)}\Rightarrow\Rightarrow Sistema\ tipo\ uno \Rightarrow\boldsymbol K_{\boldsymbol v} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\boldsymbol s\boldsymbol G\left(\boldsymbol s\right)=\boldsymbol K \Rightarrow\boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol r\boldsymbol a\boldsymbol m\boldsymbol p) = \frac{1}{\boldsymbol K}=\boldsymbol constanteSistema\ tipo\ dos\ o\ mayor\Rightarrow N=2,3...\Rightarrow\boldsymbol G\left(\boldsymbol s\right) = \boldsymbol K\frac{(\boldsymbol T_{\boldsymbol a}\boldsymbol s + 1)(\boldsymbol T_{\boldsymbol b}\boldsymbol s + 1)\ldotp \ldotp \ldotp (\boldsymbol T_{\boldsymbol m}\boldsymbol s + 1)}{\boldsymbol s^{\boldsymbol N}(\boldsymbol T_1\boldsymbol s + 1)(\boldsymbol T_2\boldsymbol s + 1)\ldotp \ldotp \ldotp (\boldsymbol T_{\boldsymbol p}\boldsymbol s + 1)}\Rightarrow\Rightarrow Sistema\ tipo\ dos\ o\ mayor\ \Rightarrow\boldsymbol K_{\boldsymbol v} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\boldsymbol s\boldsymbol G\left(\boldsymbol s\right)=\mathbf \infty \Rightarrow\boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol r\boldsymbol a\boldsymbol m\boldsymbol p) = \frac{1}{\mathbf \infty }=\boldsymbol 0Resumiendo:
El Error en Estado Estable de un sistema de control ante una entrada rampa unitaria, ess (ramp) , es:
\bigtriangleup\ \boldsymbol S\boldsymbol i\boldsymbol s\boldsymbol t\boldsymbol e\boldsymbol m\boldsymbol a\ \boldsymbol T\boldsymbol i\boldsymbol p\boldsymbol o\ 0\Rightarrow \boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol r\boldsymbol a\boldsymbol m\boldsymbol p) = \mathbf \infty \bigtriangleup \ \boldsymbol S\boldsymbol i\boldsymbol s\boldsymbol t\boldsymbol e\boldsymbol m\boldsymbol a\ \boldsymbol T\boldsymbol i\boldsymbol p\boldsymbol o\ 1\Rightarrow \boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol r\boldsymbol a\boldsymbol m\boldsymbol p) = \frac{1}{\boldsymbol K_{\boldsymbol v}};\ \ \ \ \boldsymbol K_{\boldsymbol v} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\boldsymbol s\boldsymbol G\left(\boldsymbol s\right) \bigtriangleup \boldsymbol S\boldsymbol i\boldsymbol s\boldsymbol t\boldsymbol e\boldsymbol m\boldsymbol a\ \boldsymbol T\boldsymbol i\boldsymbol p\boldsymbol o\ 2\ o\ mayor\Rightarrow \boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol r\boldsymbol a\boldsymbol m\boldsymbol p) = 0G(s) : Función de transferencia de trayectoria directa.
Error en Estado Estable ante una entrada Función Parábola
Cuando la entrada al sistema de control es la función parábola, calculamos el error en estado estable de la manera siguiente:
r(t) = \boldsymbol r(\boldsymbol t) = \frac{1}{2}\boldsymbol t^2\ \mathop{\leftrightarrow}\limits^{{\mathcal{L}}}\ \boldsymbol R(\boldsymbol s) = \frac{1}{\boldsymbol s^3}e_{ss} = \lim_{s\rightarrow 0}s\left(\frac{1}{1 + G(s)}\right)\left(\frac{1}{\boldsymbol s^3}\right) = \lim_{s\rightarrow 0}\left(\frac{1}{1 + G(s)}\right)\left(\frac{1}{\boldsymbol s^2}\right) \Rightarrow \Rightarrow \boldsymbol e_{\boldsymbol s\boldsymbol s} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\frac{1}{\boldsymbol s^2 + \boldsymbol s^2\boldsymbol G(\boldsymbol s)}= \frac{1}{ \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\boldsymbol s^2\boldsymbol G(\boldsymbol s)}Por conveniencia práctica hacemos la siguiente definición:
Se denomina Constante de Error Parabólico, Ka , (o constante de aceleración, «acceleration constant» ) a la siguiente expresión:
\boldsymbol K_{\boldsymbol a} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\boldsymbol s^2\boldsymbol G(\boldsymbol s)Por lo tanto:
El Error en Estado Estable de un sistema de control ante una entrada parabólica, ess (parabola) , es:
\boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol p\boldsymbol a\boldsymbol r\boldsymbol a\boldsymbol b\boldsymbol o\boldsymbol l\boldsymbol a) = \frac{1}{\boldsymbol K_{\boldsymbol a}}Sistema\ tipo\ cero\ o\ uno\Rightarrow N=0, 1. \Rightarrow\boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol p\boldsymbol a\boldsymbol r\boldsymbol a\boldsymbol b\boldsymbol o\boldsymbol l\boldsymbol a) = \mathbf \infty Sistema\ tipo\ dos\Rightarrow N=2 \Rightarrow\boldsymbol G\left(\boldsymbol s\right) = \boldsymbol K\frac{(\boldsymbol T_{\boldsymbol a}\boldsymbol s + 1)(\boldsymbol T_{\boldsymbol b}\boldsymbol s + 1)\ldotp \ldotp \ldotp (\boldsymbol T_{\boldsymbol m}\boldsymbol s + 1)}{\boldsymbol s^{\boldsymbol 2}(\boldsymbol T_1\boldsymbol s + 1)(\boldsymbol T_2\boldsymbol s + 1)\ldotp \ldotp \ldotp (\boldsymbol T_{\boldsymbol p}\boldsymbol s + 1)}\Rightarrow\Rightarrow\boldsymbol K_{\boldsymbol a} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\boldsymbol s^2\boldsymbol G(\boldsymbol s)=\boldsymbol K \Rightarrow\boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol p\boldsymbol a\boldsymbol r\boldsymbol a\boldsymbol b\boldsymbol o\boldsymbol l\boldsymbol a) = \frac{1}{\boldsymbol K}=constanteSistema\ tipo\ tres\ o\ mayor\Rightarrow N=3, 4, ... \Rightarrow\boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol p\boldsymbol a\boldsymbol r\boldsymbol a\boldsymbol b\boldsymbol o\boldsymbol l\boldsymbol a) = \mathbf 0 Resumiendo:
El Error en Estado Estable de un sistema de control ante una entrada parábola ess (parabola) , es:
\bigtriangleup \ \boldsymbol S\boldsymbol i\boldsymbol s\boldsymbol t\boldsymbol e\boldsymbol m\boldsymbol a\ Tipo\ 0\ ó\ 1\Rightarrow \boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol p\boldsymbol a\boldsymbol r\boldsymbol a\boldsymbol b\boldsymbol o\boldsymbol l\boldsymbol a) = \mathbf \infty \bigtriangleup \boldsymbol S\boldsymbol i\boldsymbol s\boldsymbol t\boldsymbol e\boldsymbol m\boldsymbol a\ Tipo\ 2\Rightarrow \boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol p\boldsymbol a\boldsymbol r\boldsymbol a\boldsymbol b\boldsymbol o\boldsymbol l\boldsymbol a) = \frac{1}{\boldsymbol K_{\boldsymbol a}}; \ \ \ \ \boldsymbol K_{\boldsymbol a} = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow 0}\boldsymbol s^2\boldsymbol G(\boldsymbol s) \bigtriangleup \ \boldsymbol S\boldsymbol i\boldsymbol s\boldsymbol t\boldsymbol e\boldsymbol m\boldsymbol a\ Tipo\ 3\ o\ mayor\Rightarrow \boldsymbol e_{\boldsymbol s\boldsymbol s}(\boldsymbol p\boldsymbol a\boldsymbol r\boldsymbol a\boldsymbol b\boldsymbol o\boldsymbol l\boldsymbol a) = 0 G(s) : Función de transferencia de trayectoria directa.
Te puede interesar:
- Se resuelven ejercicios de Señales y Sistemas, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…
Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos. Al suscribirte podrás contar con excelente material para estudiar y superar con éxito las demandas académicas.
Curso relacionado:
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs
