La integral de convolución permite calcular directamente la señal de salida y(t) de cualquier sistema LIT para el cual se conoce su respuesta al impulso h(t) , y ante cualquier señal de entrada x(t) . La respuesta al impulso de un sistema LIT por lo tanto, describe el sistema en su conjunto, permitiendo así su caracterización completa.
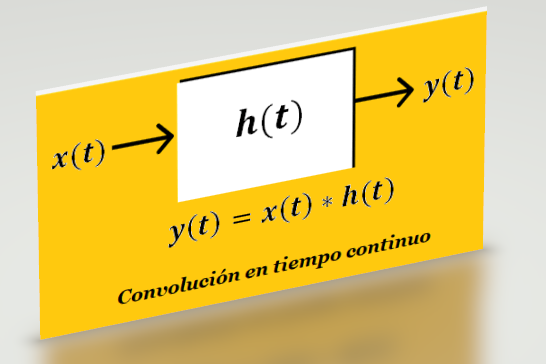
Concepto de Convolución
Sea h(t) la respuesta al impulso de un sistema Lineal e Invariante en el Tiempo (Sistema LIT) cuya salida es y(t). Si es la entrada a dicho sistema es la señal x(t)=0 para t<0, entonces la salida y(t) puede ser determinada mediante una operación entre su señal de entrada x(t) y su respuesta al impulso h(t). Dicha operación es conocida como «Integral de Convolución«:
\boldsymbol y(\boldsymbol t) = \boldsymbol x(\boldsymbol t)*\boldsymbol h(\boldsymbol t) = \int\limits_0^{\boldsymbol t}\boldsymbol x(\boldsymbol \tau )\boldsymbol h(\boldsymbol t - \boldsymbol \tau )\mathbf d\boldsymbol \tau ;\ \ \ \ \ \ \ (1)Dónde:
\boldsymbol *:operador\ de\ Convolución
La operación de convolución es conmutativa, por lo que:
\boldsymbol y\left(\boldsymbol t\right) = \boldsymbol x\left(\boldsymbol t\right)*\boldsymbol h(\boldsymbol t) = \boldsymbol h(\boldsymbol t)*\boldsymbol x(\boldsymbol t);\ \ \ \ \ \ \ (2)
Es decir:
\boldsymbol y(\boldsymbol t) =\int\limits_0^{\boldsymbol t}\boldsymbol x(\boldsymbol \tau )\boldsymbol h(\boldsymbol t - \boldsymbol \tau )\mathbf d\boldsymbol \tau = \int\limits_0^{\boldsymbol t}\boldsymbol h\left(\boldsymbol \tau \right)\boldsymbol x\left(\boldsymbol t - \boldsymbol \tau \right)\mathbf d\boldsymbol \tau;\ \ \ \ \ \ \ (3)Relación entre la integral de convolución y la función de transferencia
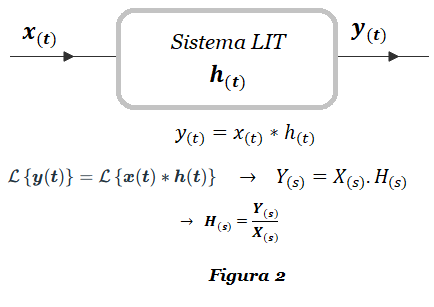
Aplicaremos la Transformada de Laplace a ambos lados de la ecuación (2):
\mathbf{\mathcal{L}}\left\{\boldsymbol y(\boldsymbol t)\right\} = \mathbf{\mathcal{L}}\left\{\boldsymbol x(\boldsymbol t)*\boldsymbol h(\boldsymbol t)\right\}Y obtenemos la ecuación (4):
\boldsymbol Y(\boldsymbol s) = \boldsymbol X(\boldsymbol s)H(\boldsymbol s);\ \ \ \ \ \ (4)
La ecuación (4) nos permite obtener la Función de Transferencia del Sistema :
\boldsymbol H(\boldsymbol s) = \frac{Y(\boldsymbol s)}{X(\boldsymbol s)};\ \ \ \ \ \ (5)La ecuación (5) tiene una consecuencia muy importante para la ingeniería en general, y es que conociendo la relación entrada-salida de un sistema LIT, tenemos todo lo necesario para determinar la respuesta impulsiva de dicho sistema de una manera algebraica (evitando el cálculo de integrales), lo cual representa una de las grandes ventajas de utilizar la Transformada de Laplace.
La Figura 2 resume la relación entre la integral de convolución y la función de transferencia:
Pasos para calcular la integral de convolución – Método Gráfico
Para calcular la convolución entre x(t) y h(t) , ecuación (2), es de gran utilidad graficar las funciones de la integral de convolución. El primer paso consiste en graficar x(τ) y h(t-τ) (ambas señales en función de τ : tau). Luego, determinar las regiones donde ocurre solapamiento entre ambas señales para calcular la integral del producto x(τ) .h(t-τ) en cada una de estas regiones (recordar que podemos elegir la opción x(t-τ) .h(τ) dependiendo de la que nos sea más fácil o conveniente). Para determinar la forma apropiada del producto y de los límites de integración, debemos desplazar la gráfica de h(t-τ) (o de x(t-τ) ) de izquierda a derecha y determinar como se modifica el solapamiento.
En fin, los pasos para determinar la integral de convolución de la ecuación (2) se pueden resumir de la siguiente manera:
- Graficar x(τ) y h(-τ) (ambas señales en función de τ : tau). La función h(-τ) es igual a la función h(τ) reflejada sobre el eje vertical.
- Graficar h(t-τ) para un valor cualquiera de t, tal como t<0. Observar que h(t-τ) es igual que h(-τ) desplazada de tal forma que el origen de la gráfica se encuentra en τ =t.
- Desplazar h(t-τ) de izquierda a derecha. Determinar el producto x(τ) . h(t-τ) en las regiones de solapamiento (fuera de estas regiones el producto entre ambas señales es igual a cero).
- Integrar el producto x(τ) . h(t-τ) en cada una de las regiones de solapamiento por separado.
- Finalmente sumar el resultado de cada integración del paso anterior.
Convolución con la señal impulso unitario.
Observe la redundancia de decir que, si x(t) es un impulso unitario, entonces, para un sistema LTI, y(t) = h(t) . Se establece así una importante propiedad de la convolución con el impulso unitario:
\boldsymbol y(\boldsymbol t) = \boldsymbol \delta (\boldsymbol t)*\boldsymbol h(\boldsymbol t) = \boldsymbol h(\boldsymbol t)
En general podemos asegurar por definición que:
\boldsymbol x(\boldsymbol t)*\boldsymbol \delta (\boldsymbol t) = \boldsymbol x\left(\boldsymbol t\right) ;\ \ \ \ \ \ (6)
DEMOSTRACIÓN: La función impulso unitario δ(t) , también conocida como Delta de Dirac, tiene un papel fundamental en el análisis de señales.
La función impulso unitario está definida de la siguiente manera :
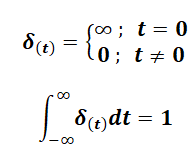
Esta señal se puede ver como un pulso rectangular de área unidad, ancho ε y altura 1/ε , tal como se muestra en la Figura 3:
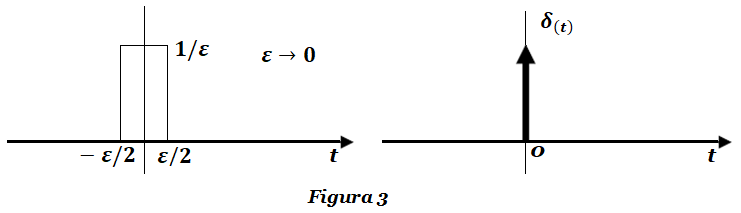
Como se puede ver en la Figura 3, la función impulso unitario es una función par, es decir:
\boldsymbol \delta \left(\boldsymbol t\right) = \boldsymbol \delta \left(\boldsymbol - \boldsymbol t\right)
La función impulso unitario no es una función en el sentido ordinario como se define una función. Una función ordinaria viene especificada para todos sus valores de tiempo t. la función impulso unitario es cero para todo valor de t, excepto en t=0, y este es el único punto interesante de su dominio, y sin embargo aquí su valor es indefinido. Más útil es definir la función impulso unitario como una función generalizada.
Una función generalizada se define por sus efectos sobre otras funciones, en vez de ser definida por los valores que asume en su dominio. En este caso, la función impulso unitario se define sobre todo por su propiedad de muestreo y por su propiedad de selección.
La Función Impulso Unitario δ(t) está mejor definida por sus aplicaciones que por los valores que asume en su dominio.
Propiedad de muestreo : Supongamos la multiplicación entre la función δ(t) y una función cualquiera Φ(t) continua en t=0, donde la función tiene una magnitud Φ(0). Se obtiene que:
\boldsymbol \phi (\boldsymbol t)\ldotp \boldsymbol \delta (\boldsymbol t) = \boldsymbol \phi \left(0\right)\ldotp \boldsymbol \delta \left(\boldsymbol t\right)
Se puede generalizar este resultado para una función impulso unitario desplazado en t=t0 :
\boldsymbol \phi (\boldsymbol t)\ldotp \boldsymbol \delta (\boldsymbol t - \boldsymbol t_0) = \boldsymbol \phi \left(\boldsymbol t_0\right)\ldotp \boldsymbol \delta \left(\boldsymbol t - \boldsymbol t_0\right) ;\ \ \ \ \ \ (7)
La ecuación (7) es de suma importancia en el análisis de señales y sistemas y se conoce como La propiedad de Muestreo del Impulso Unitario.
Propiedad de selección : Integrando el resultado de la propiedad anterior y utilizando la definición del impuso unitario dado anteriormente, obtenemos que:
\int\limits_{- \mathbf \infty}^{\mathbf \infty}\boldsymbol \phi (\boldsymbol t)\ldotp \boldsymbol \delta (\boldsymbol t)\mathbf d\boldsymbol t = \int\limits_{- \mathbf \infty}^{\mathbf \infty}\boldsymbol \phi (0)\ldotp \boldsymbol \delta (\boldsymbol t)\mathbf d\boldsymbol t = \boldsymbol \phi (0)\ldotp \int\limits_{- \mathbf \infty}^{\mathbf \infty}\boldsymbol \delta (\boldsymbol t)\mathbf d\boldsymbol t = \boldsymbol \phi (0)Se puede generalizar este resultado para una función impulso unitario desplazado en t=t0 :
\int\limits_{- \mathbf \infty}^{\mathbf \infty}\boldsymbol \phi (\boldsymbol t)\ldotp \boldsymbol \delta (\boldsymbol t - \boldsymbol t_0)\mathbf d\boldsymbol t = \int\limits_{- \mathbf \infty}^{\mathbf \infty}\boldsymbol \phi (\boldsymbol t_0)\ldotp \boldsymbol \delta (\boldsymbol t - \boldsymbol t_0)\mathbf d\boldsymbol t = \boldsymbol \phi (\boldsymbol t_0)\ldotp \int\limits_{- \mathbf \infty}^{\mathbf \infty}\boldsymbol \delta (\boldsymbol t - \boldsymbol t_0)\mathbf d\boldsymbol t = \boldsymbol \phi (\boldsymbol t_0)Es decir:
\int\limits_{- \mathbf \infty}^{\mathbf \infty}\boldsymbol \phi (\boldsymbol t)\ldotp \boldsymbol \delta (\boldsymbol t - \boldsymbol t_0)\mathbf d\boldsymbol t = \boldsymbol \phi (\boldsymbol t_0) ;\ \ \ \ \ \ (8)La ecuación (8) es de igual importancia en el análisis de señales y sistemas y se conoce como La propiedad de Selección del Impulso Unitario.
En consecuencia, tomando en cuenta que la función impulso unitario es una función par, y tomando en cuenta la propiedad de selección, queda demostrado que:
\boldsymbol x(\boldsymbol t)*\boldsymbol \delta (\boldsymbol t) = \int\limits_{- \mathbf \infty}^{\mathbf \infty}\boldsymbol x(\boldsymbol \tau )\boldsymbol \delta (\boldsymbol t - \boldsymbol \tau )\mathbf d\boldsymbol \tau = \boldsymbol x\left(\boldsymbol t\right)\int\limits_{- \mathbf \infty}^{\mathbf \infty}\boldsymbol \delta \left(\boldsymbol t - \boldsymbol \tau \right)\mathbf d\boldsymbol \tau = \boldsymbol x\left(\boldsymbol t\right)También se puede demostrar que, en general:
\boldsymbol x(\boldsymbol t)*\boldsymbol \delta (\boldsymbol t - \boldsymbol t_0) = \boldsymbol x\left(\boldsymbol t - \boldsymbol t_0\right);\ \ \ \ \ \ (9)
La ecuación (9) es otra importante herramienta analítica y estipula que el desplazamiento horizontal arbitrario de cualquier señal x(t) se puede expresar como el resultado de la convolución de dicha señal no desplazada con un impulso unitario sujeto a este desplazamiento. Es decir:
\boldsymbol x\left(\boldsymbol t - \boldsymbol t_0\right) = \boldsymbol x(\boldsymbol t)*\boldsymbol \delta (\boldsymbol t - \boldsymbol t_0)
Si la señal x(t) es una señal periódica de período fundamental T0, podemos utilizar la ecuación (9) para expresar dicha señal como la convolución de su período básico x0(t) (es decir, la forma de la curva de la función en un intervalo de tiempo igual a su período) con un tren de deltas de su mismo período fundamental:
\boldsymbol x\left(\boldsymbol t\right) = \boldsymbol x_0(\boldsymbol t)*\sum_{\boldsymbol m = - \mathbf \infty}^{\mathbf \infty}\boldsymbol \delta (\boldsymbol t - \boldsymbol m\boldsymbol T_0);\ \ \ m \in {\mathbb{Z}}Ejercicios resueltos de Convolución en tiempo continuo
En construcción… .
Ejercicio CV-1: Un sistema LIT de tiempo continuo genera la siguiente señal h(t) como respuesta al impulso:
\boldsymbol h(\boldsymbol t) = 5\boldsymbol e^{- \boldsymbol t}\boldsymbol u(\boldsymbol t)Considerando la señal x(t) como señal de entrada a dicho sistema:
\boldsymbol x\left(\boldsymbol t\right) = \left(\mathbf t - 2\right)^2\ldotp \left[\boldsymbol u\left(\boldsymbol t - 2\right) - \boldsymbol u\left(\boldsymbol t - 4\right)\right]
Calcular:
- Los instantes inicial y final de la señal de salida y(t) sin evaluar la integral de convolución;
- La salida y(t) ejecutando la integral de convolución (método gráfico).
- Comprobar el resultado en Matlab.
Encontrarás la solución al ejercicio CV-1 en el siguiente link: SOLUCIÓN Ejercicio CV-1.
Ejercicio FT-2: Obtener la función de transferencia H1(s)=X1(s)/U(s) y H2(s)=X2(s)/U(s) del sistema masa-resorte-amortiguador de la Figura 2.
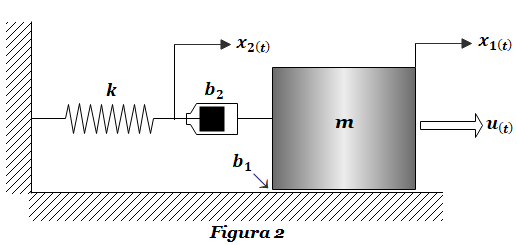
Encontrarás la solución al ejercicio FT-2 en el siguiente link: SOLUCIÓN Ejercicio FT-2.
Ejercicio FT-3: Obtener la función de transferencia H1(s)=X1(s)/U(s) y H2(s)=X2(s)/U(s) del sistema masa-resorte-amortiguador de la Figura 3. Ilustrar el uso de diagramas de cuerpo libre..
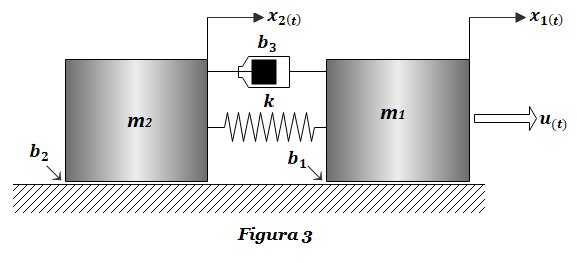
Encontrarás la solución al ejercicio FT-3 en el siguiente link: SOLUCIÓN Ejercicio FT-3.
Ejercicio FT-4: Obtener la función de transferencia G(s)=Eo(s)/Ei(s) del sistema eléctrico de la Figura 4. La salida es la caída de voltaje e0(t) en los nodos del capacitor, mientras que la entrada es la tensión ei(t) . Aplicar el método de mallas para determinar las ecuaciones diferenciales que representan el modelo del sistema y obtener G(s) a partir de ellas.
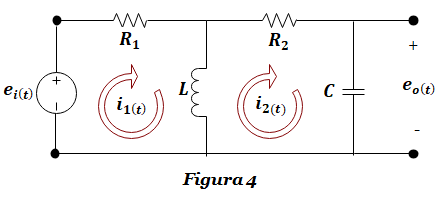
Encontrarás la solución al ejercicio FT-4 en el siguiente link: SOLUCIÓN Ejercicio FT-4.
PROBLEMA 1.1: Calcula la expresión de la salida v0(t) en función del tiempo para el circuito RLC de la Figura 1, ante una entrada vi(t)=u0(t) (escalón unitario) con R=2 Ω, L=1 H y C=1/5 F. Considere las condiciones iniciales iguales a cero.
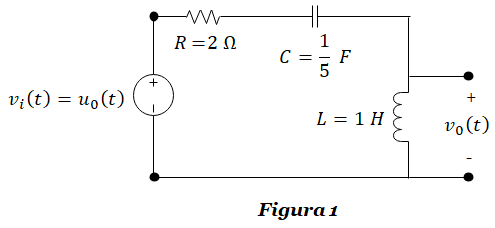
Encontrarás la solución al Problema 1-1 en el siguiente link: SOLUCIÓN Examen 1-1.
Te puede interesar:
- Se resuelven ejercicios de Señales y Sistemas, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…
Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos. Al suscribirte podrás contar con excelente material para estudiar y superar con éxito las demandas académicas.
Curso relacionado:
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs
