Determinar FT de Sistema MRA Rotacional – E14
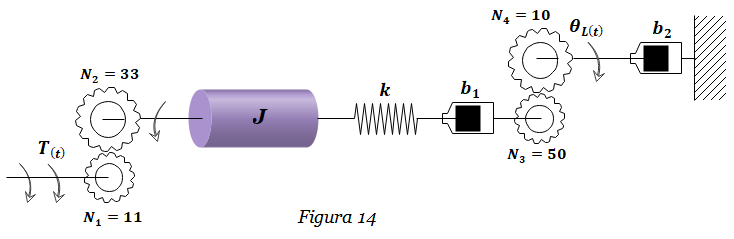
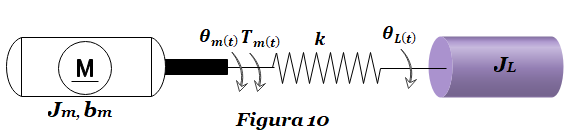
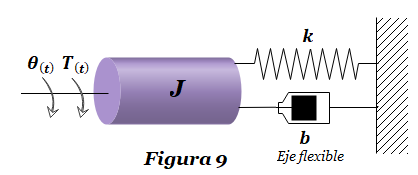
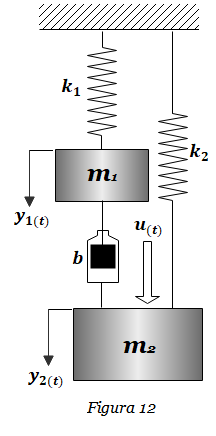
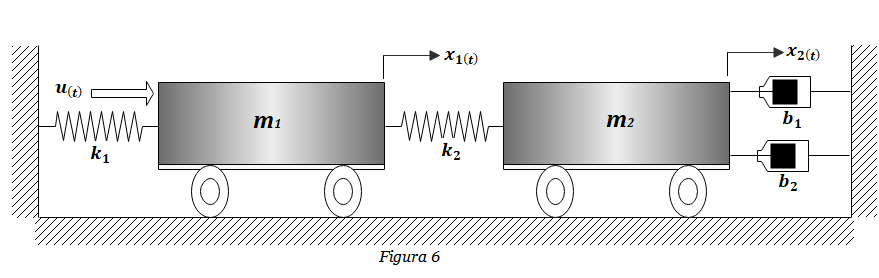
Ejercicio FT-14: Obtener la función de transferencia H(s)=θL(s)/T(s) del sistema masa-resorte-amortiguador de la Figura 14. La salida es el desplazamiento θL(t) del sistema, mientras que la entrada es el Torque T(t) que se ejerce sobre la masa inercial J . Considerar k=3 N-m/rad, b1=2, b2=0.04 N-m-s/rad, J=1 Kg-m2. En primer lugar se determinan las ecuaciones […]
Determinar FT de Sistema MRA Rotacional – E14 Leer más »