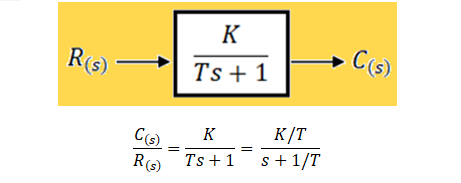
Un sistema de control a lazo abierto para un sistema de primer orden, nos permite aumentar o disminuir la ganancia estática k del sistema, pero no nos permite cambiar su constante de tiempo T. Por el contrario, En cambio, con un sistema de control a lazo cerrado para un sistema de primer orden, podemos variar ambos parámetros.
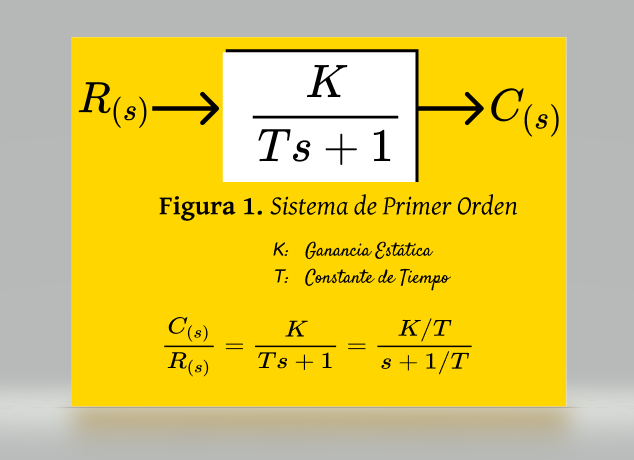
Ejercicio SCA-1: Aplicar un sistema de control a lazo abierto a la planta cuya función de transferencia (FT) es Gp(s) . Utilizar un controlador proporcional con FT Gc(s). Simular en Matlab la respuesta para los siguientes valores de la ganancia del controlador, K =1,2,3 y 4 con el fin de mostrar el cambio en los parámetros k y T de la planta Gp(s). Aplicar luego un sistema de control a lazo cerrado a la planta Gp(s) y simular su respuesta para los mismos valores de K. Mostrar los cambios en los parámetros k y T .
Función\ de\ Transferencia \ de\ la\ planta:\ \ \ \boldsymbol G_{\boldsymbol p}(\boldsymbol s) = \frac{2.9276}{\boldsymbol s + 0.2336}Diagrama de bloques del sistema de control.
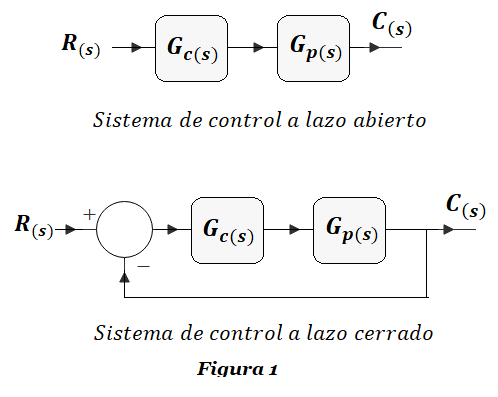
La figura 1 muestra ambos casos representados por diagramas de bloques, un sistema de control a lazo abierto y otro a lazo cerrado. Los elementos básicos son el controlador proporcional, cuya función de transferencia (FT) es Gc(s), y la planta cuya FT es Gp(s).
(Para un repaso de Diagramas de Bloques ver: Diagrama de Bloques)
Veamos que pasa considerando los siguientes valores:
Función\ de\ Transferencia \ del\ controlador:\ \ \ \boldsymbol G_{\boldsymbol c}(\boldsymbol s) = \boldsymbol K\boldsymbol ;\ \ \ \ 0 < K < 5\boldsymbol G_{\boldsymbol p}(\boldsymbol s) = \frac{2.9276}{\boldsymbol s + 0.2336}Observamos que la planta es un sistema de primer orden.
Sistema de primer orden a lazo abierto
Para el sistema a lazo abierto de la figura 1 se cumple que:
\frac{\boldsymbol C(\boldsymbol s)}{\boldsymbol R(\boldsymbol s)} = \boldsymbol G_{\boldsymbol c}(\boldsymbol s)\ldotp \boldsymbol G_{\boldsymbol p}\left(\boldsymbol s\right) = \boldsymbol K. \frac{2.9276}{\boldsymbol s + 0.2336}Atención: No confundir la K del controlador con la k (ganancia estática) del sistema.
El siguiente script en Matlab muestra como varía la respuesta (salida) del sistema en lazo abierto a la entrada escalón unitario, R(s)=u(t), a medida que la ganancia del controlador K adquiere los siguientes valores:1,2,3 y 4.
G=tf([2.9276],[1 0.2336]);
K=[1 2 3 4];
G1=K(1)*G; G2=K(2)*G;
G3=K(3)*G; G4=K(4)*G;
step(G1,G2,G3,G4)legend(‘K=1′,’K=2′,’K=3′,’K=4’)
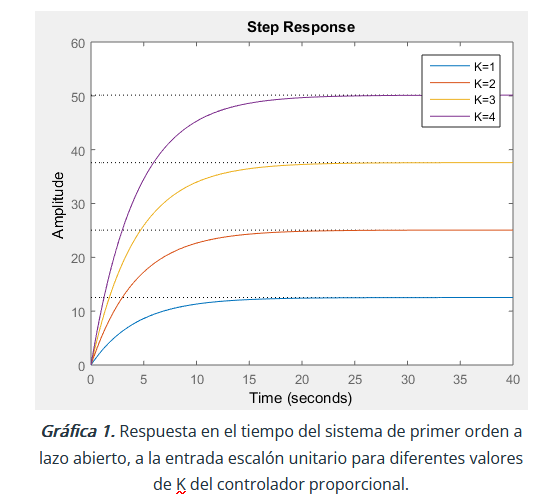
En la gráfica 1 podemos observar como varía la salida del sistema a medida que cambia la ganancia K del controlador. Notamos que aumenta la Ganancia Estática k del sistema de primer orden a medida que aumenta la K del controlador. Sin embargo, en cada caso, la Constante de Tiempo T se mantiene constante. Utilizando el modelo general de FT para un sistema de primer orden y la FT de la planta, podemos calcular el valor de la Constante de Tiempo T :
Modelo\ general\ FT \ sistema\ 1er\ orden:\ \ \ \boldsymbol G(\boldsymbol s) = \frac{\boldsymbol k}{\boldsymbol T\boldsymbol s + 1}\boldsymbol G_{\boldsymbol p}(\boldsymbol s) = \frac{2.9276}{\boldsymbol s + 0.2336}=\frac{1}{0.2336}(\frac{2.9276}{\frac{1}{0.2336}s + 1})\Rightarrow\frac{12.53}{4.3\boldsymbol s + 1}=\frac{\boldsymbol k}{\boldsymbol T\boldsymbol s + 1}Constante\ de\ tiempo:\ \ \ \ \ \boldsymbol T = \boldsymbol4.3\ s
Utilizando la simulación de la gráfica 1, en la gráfica 2 hemos calculado el valor de la constante T, que es el tiempo en que cada sistema alcanza el 63,2% de su valor final. Los valores finales para cada valor del controlador se muestran en la gráfica 3. Como ejemplo de este procedimiento tomamos el sistema G1:
valor\ del\ controlador:\ K = 1\Rightarrow valor\ de\ la\ ganancia\ estática:\ \boldsymbol k_1 = 12.5, \ gráfica\ 3,\ sistema\ G_1
k_1 = 12.5\Rightarrow 63.2\% = (0.632) \times 12.5 = 7.9: amplitud\ del\ sistema\ G_1,\ gráfica\ 2, \cuando\ t=constante\ de\ tiempo
Moviendo el cursor del ratón sobre la gráfica generada por Matlab podemos ubicar y apuntar este valor de amplitud sobre la curva (System G1, Amplitude 7.98). De inmediato vemos que el tiempo generado por la gráfica coincide con el valor calculado para la constante de tiempo T (Time:4.34 s). Igual cálculo podríamos hacer para el resto de los sistemas: G2,G3 y G4.
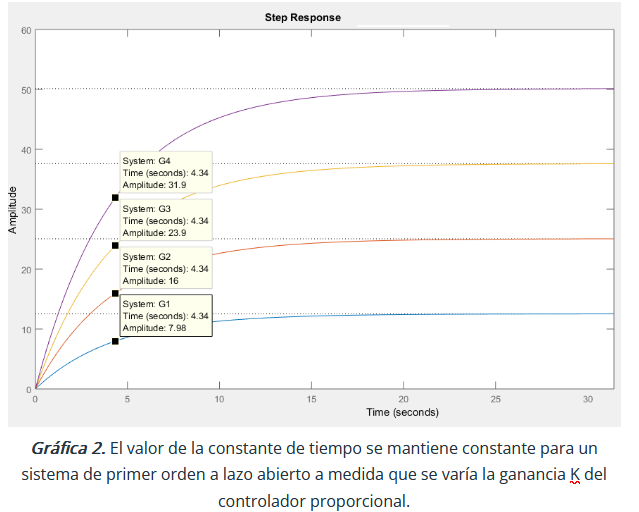
Observamos en la gráfica 2 que el valor de la Constante de Tiempo no varía a pesar de que varía el valor de la Ganancia Estática a medida que varía el valor de la ganancia del controlador proporcional:
K = 2\Rightarrow valor\ de\ la\ ganancia\ estática:\ \boldsymbol k_2 = 25.1, \ gráfica\ 3,\ sistema\ G_2
K = 3\Rightarrow valor\ de\ la\ ganancia\ estática:\ \boldsymbol k_2 = 37.6, \ gráfica\ 3,\ sistema\ G_3
K = 4\Rightarrow valor\ de\ la\ ganancia\ estática:\ \boldsymbol k_2 = 50.1, \ gráfica\ 3,\ sistema\ G_4
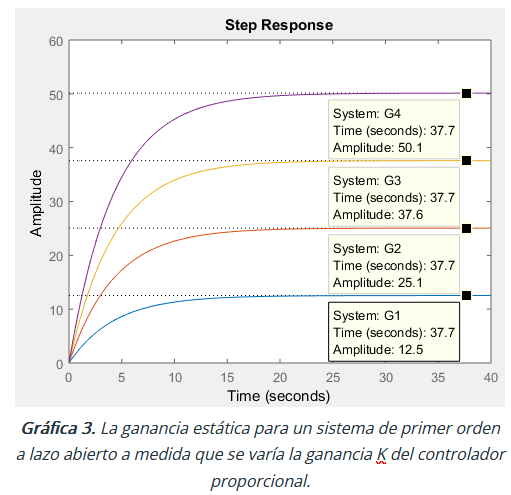
Demostramos de esta manera que el sistema de control a lazo abierto no logra modificar el valor de la Constante de Tiempo de un sistema de primer orden cuando responde ante una entrada escalón unitario.
La mayoría de los sistemas prácticos necesitan sin embargo, mayor control sobre ambos parámetros. Por ello se recurre al lazo cerrado.
Sistema de primer orden a lazo cerrado
Aplicando álgebra de bloques al sistema a lazo cerrado de la Figura 1, obtenemos que:
\boldsymbol s\boldsymbol y\boldsymbol s = \frac{\boldsymbol C(\boldsymbol s)}{\boldsymbol R(\boldsymbol s)} = \frac{\boldsymbol G_{\boldsymbol c}(\boldsymbol s) \times \boldsymbol G_{\boldsymbol p}(\boldsymbol s)}{1 + \boldsymbol G_{\boldsymbol c}\left(\boldsymbol s\right) \times \boldsymbol G_{\boldsymbol p}\left(\boldsymbol s\right)} = \frac{2.9276 \times \boldsymbol K}{\boldsymbol s + 0.2336 + 2.9276 \times \boldsymbol K}El siguiente script en Matlab muestra como varía la respuesta (salida) del sistema en lazo cerrado a la entrada escalón unitario a medida que la ganancia del controlador K adquiere los valores 1,2,3 y 4:
G=tf([2.9276],[1 0.2336]); K=[1 2 3 4]; G1=K(1)*G; G2=K(2)*G; G3=K(3)*G; G4=K(4)*G;
sys1=feedback(G1,1);
sys2=feedback(G2,1);
sys3=feedback(G3,1);
sys4=feedback(G4,1);
step(sys1,sys2,sys3,sys4)
legend(‘K1=1′,’K2=2′,’K3=3′,’K4=4’)
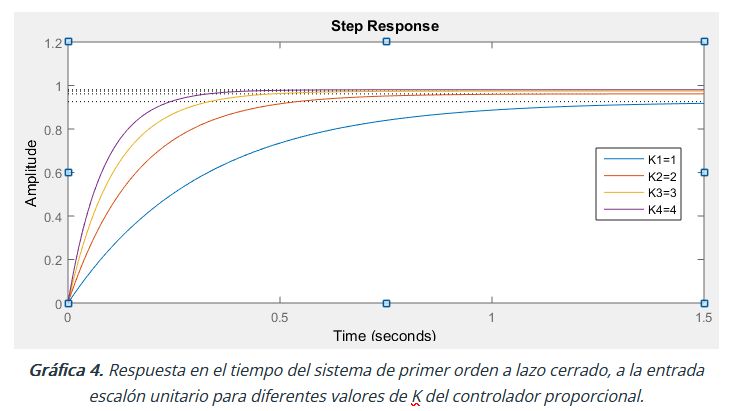
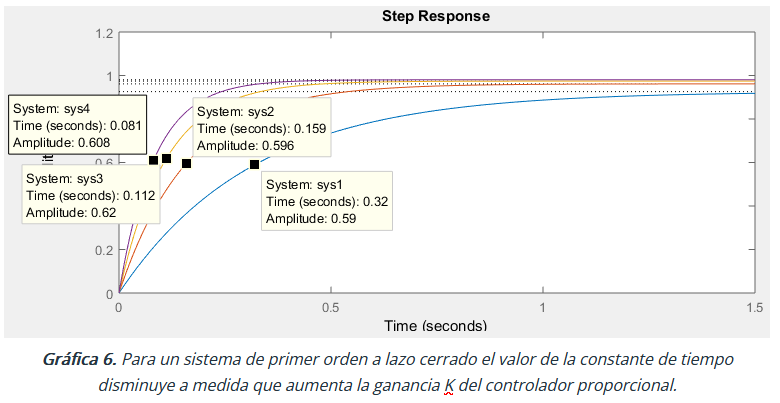
La gráfica 4 muestra como el sistema es más rápido a medida que la ganancia K del controlador aumenta. Es decir, la constante de tiempo T del sistema de primer orden en lazo cerrado disminuye a medida que la ganancia K del controlador aumenta:
\boldsymbol K = 1\ \ \ \ \Rightarrow \boldsymbol s\boldsymbol y\boldsymbol s_1 = \frac{2.9276}{\boldsymbol s + 3.1612}\Rightarrow \ \ \ \ \boldsymbol T_1 = \frac{1}{3.1612} = 0.32\boldsymbol\ s\boldsymbol K = 2\ \ \ \ \Rightarrow \boldsymbol s\boldsymbol y\boldsymbol s_2 = \frac{5.8552}{\boldsymbol s + 6.0888}\Rightarrow \ \ \ \ \boldsymbol T_2 = \frac{1}{6.0888} = 0.16\boldsymbol\ s\boldsymbol K = 3\ \ \ \ \Rightarrow \boldsymbol s\boldsymbol y\boldsymbol s_3 = \frac{8.7828}{\boldsymbol s + 9.0164}\Rightarrow \ \ \ \ \boldsymbol T_3 = \frac{1}{9.0164} = 0.11\boldsymbol\ s\boldsymbol K = 4\ \ \ \ \Rightarrow \boldsymbol s\boldsymbol y\boldsymbol s_4 = \frac{11.7104}{\boldsymbol s +11.944}\Rightarrow \ \ \ \ \boldsymbol T_4 = \frac{1}{11.944} = 0.08\boldsymbol\ sLos resultados anteriores (gráfica 6) muestran que para el sistema a lazo cerrado podemos utilizar la ganancia K del controlador proporcional para ajustar el sistema de tal manera que responda a una velocidad determinada. En términos del Lugar de las Raíces un sistema más rápido significa que el polo del sistema se va desplazando hacia la izquierda del eje real a medida que aumenta K, gráfica 5.
sys=feedback(G1,1);
rlocus(sys)
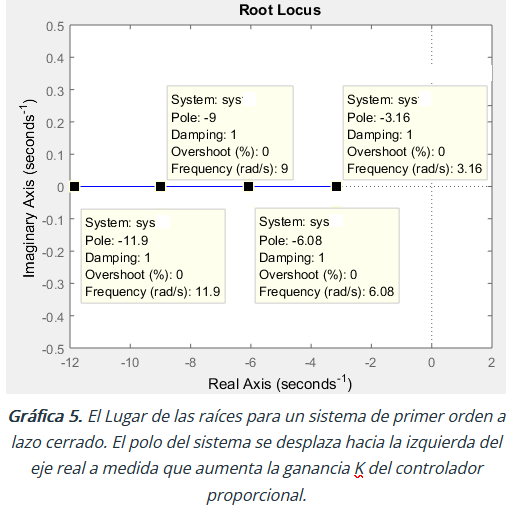
La gráfica 6 muestra la constante T de cada sistema cuyo subíndice coincide con el valor de la ganancia K del controlador. Tener siempre presente que la constante T es el tiempo en que cada sistema alcanza el 63,2% de su valor final, lo que nos lleva a descubrir un dato interesante y es que el valor final de cada sistema se acerca a uno, por lo tanto fijarse que las amplitudes de todos los sistemas sys 1, 2, 3 y 4 valen aproximadamente 0.6 en t=T. Otro aspecto importante de resaltar gracias al lazo cerrado es que una salida de valor igual o cercano a 1 significa que el sistema intenta de manera automática mantener su salida de igual valor que la entrada, sistema conocido como «seguidor de entrada», ampliamente utilizado en sistemas de control de posición. Observamos además que el valor de la ganancia estática k tiende a 1 a medida que aumentamos el valor de la ganancia K del controlador.
Te puede interesar:
- Se resuelven ejercicios de Análisis y Diseño de Sistemas de Control, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos….
Artículos relacionados:
Sistemas de Primer Orden – Teoría.
Curso Intensivo Función de Transferencia – Teoría y Práctica
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Cent