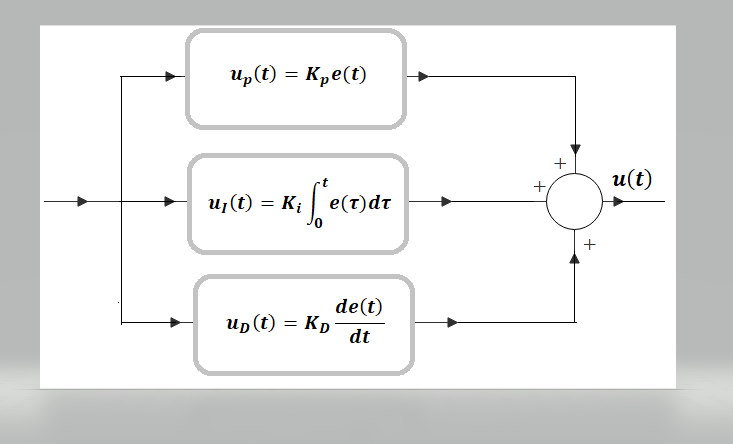
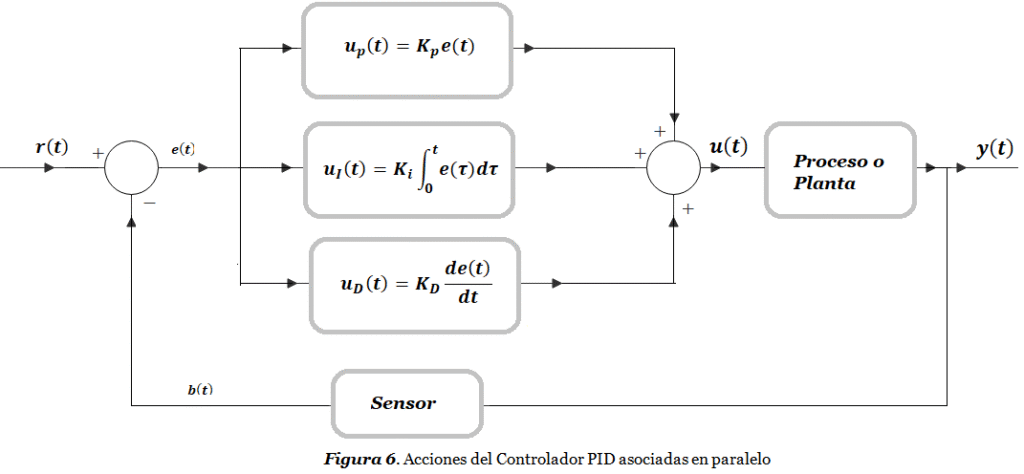
El Controlador PID es un tipo de regulador que aplica a la planta (o proceso) una señal de control u(t) compuesta por una combinación lineal de diferentes señales, tal como lo ilustra la Figura adjunta.
Ya habíamos visto en Sistema de Control que la Figura 1 representa la dinámica de un proceso lineal controlado:
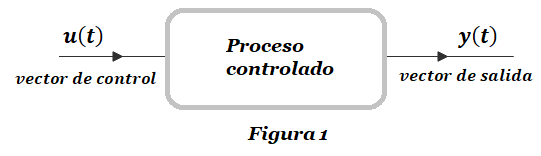
Las variables controladas están representadas por el vector de salida y(t). El objetivo de diseño es que dichas variables se comporten de manera tal que satisfagan todas las especificaciones del diseño. Este objetivo implica buscar un intervalo para la señal de control u(t), de manera tal que al actuar sobre el proceso (o planta) se genere la respuesta en el tiempo deseada.
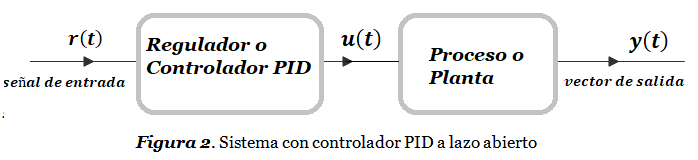
En la Figura 2 la señal de control u(t) es generada por un Controlador PID :
El Controlador PID es un tipo de regulador que aplica a la planta (o proceso) una señal de control u(t) compuesta por una combinación lineal de diferentes señales cuyas acciones se clasifican de la siguiente manera:
- acciones proporcionales (P),
- acciones integrales (i) y
- acciones derivativas (D).
Por lo general el sistema de control más básico requiere de una configuración a lazo cerrado (revisar en Sistema de Control) como el de la Figura 3. En este caso, las acciones del Controlador PID se ejecutan sobre la señal de error e(t) .
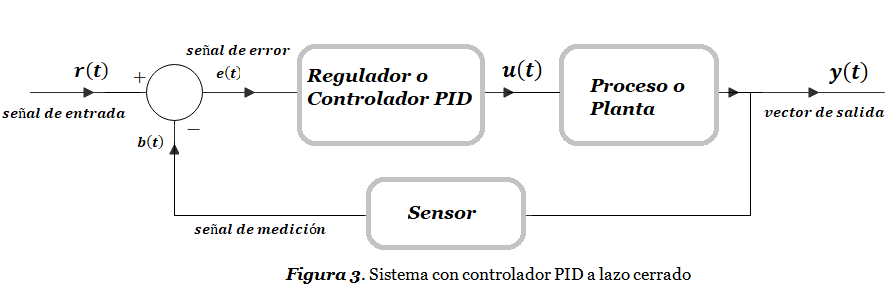
Considerando la señal de error e(t) de la Figura 3, cada una de las acciones enumeradas anteriormente se expresan matemáticamente como:
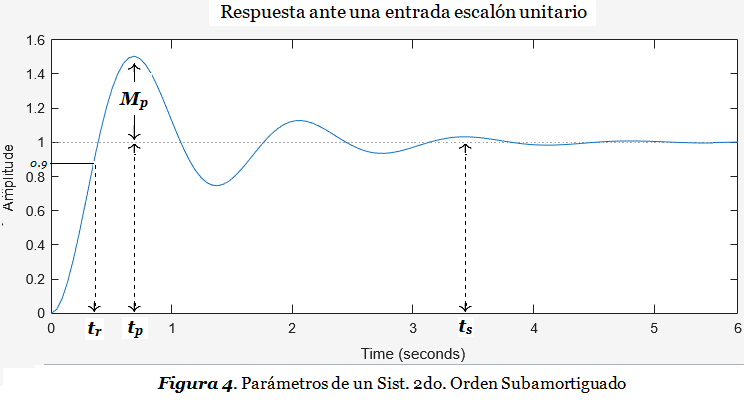
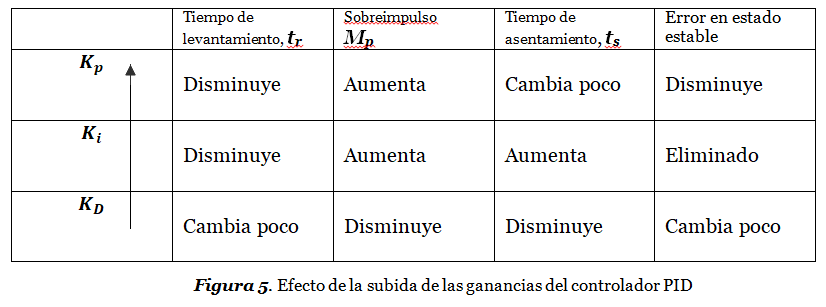
(P) \ acción\ proporcional:\ \ \ \ \boldsymbol u_{\boldsymbol p}(\boldsymbol t) = \boldsymbol K_{\boldsymbol p}\boldsymbol e(\boldsymbol t)(I) \ acción\ integral:\ \ \ \ \boldsymbol u_{\boldsymbol i}(\boldsymbol t) = \boldsymbol K_{\boldsymbol i}\int\limits_0^{\boldsymbol t}\boldsymbol e(\boldsymbol \tau )\mathbf d\boldsymbol \tau (D) \ acción\ derivativa:\ \ \ \ \boldsymbol u_{\boldsymbol D}(\boldsymbol t) = \boldsymbol K_{\boldsymbol D}\frac{\mathbf d\boldsymbol e(\boldsymbol t)}{\mathbf d\boldsymbol t} Dónde Kp , Ki , KD representan la ganancia individual de cada una de las acciones. Se verá más adelante que la subida de cada una de estas constantes tendrá los siguientes efectos sobre la respuesta en el tiempo a la entrada escalón unitario del sistema de la Figura 3 cuando la planta es un sistema de segundo orden subamortiguado:
Función de Transferencia del Controlador PID
Se decía anteriormente que la señal de control será una combinación lineal de las acciones P, I y D, por lo que la expresión matemática para la señal de control u(t) de la Figura 3 será:
u(\boldsymbol t) = \boldsymbol u_{\boldsymbol p}(\boldsymbol t) + \boldsymbol u_{\boldsymbol i}(\boldsymbol t) + \boldsymbol u_{\boldsymbol D}(\boldsymbol t)Sustituyendo obtenemos que:
\boldsymbol u\left(\boldsymbol t\right) = \boldsymbol K_{\boldsymbol p}\boldsymbol e(\boldsymbol t) + \boldsymbol K_{\boldsymbol i}\int\limits_{\boldsymbol o}^{\boldsymbol t}\boldsymbol e(\boldsymbol \tau )\mathbf d\boldsymbol \tau + \boldsymbol K_{\boldsymbol D}\frac{\mathbf d\boldsymbol e(\boldsymbol t)}{\mathbf d\boldsymbol t}\ \ \ \ (1)Al representar la sumatoria de acciones de la ecuación (1) mediante un diagrama de bloques, dichas acciones estarán asociadas en paralelo, como se muestra en la Figura 6:
Las señales del sistema de la Figura 6 por lo general pueden visualizarse fácilmente en el dominio del tiempo. En consecuencia, los métodos en el dominio del tiempo son los preferidos para diseñar Controladores PID. Lo que se busca en la práctica es seleccionar el tipo de controlador más simple que permita cumplir con las especificaciones de diseño, y simultáneamente evitar sistemas más complejos y costosos de lo necesario.
Tomamos ahora la Transformada de Laplace de la ecuación (1) :
\boldsymbol U\left(\boldsymbol s\right) = \boldsymbol K_{\boldsymbol p}\ldotp \boldsymbol E(\boldsymbol s) + \boldsymbol K_{\boldsymbol i}\ldotp \frac{\boldsymbol E\left(\boldsymbol s\right)}{\boldsymbol s} + \boldsymbol K_{\boldsymbol D}\ldotp \boldsymbol s\ldotp \boldsymbol E\left(\boldsymbol s\right)\ \ \ \ (2)La Función de Transferencia Gc(s) del Controlador PID se obtiene despejando de la ecuación (2) el cociente U(s)/E(s) :
\boldsymbol G_{\boldsymbol c}(\boldsymbol s) =\frac{\boldsymbol U\left(\boldsymbol s\right)}{E\left(\boldsymbol s\right)} = \boldsymbol K_{\boldsymbol p} + \boldsymbol K_{\boldsymbol i}\ldotp \frac{1}{\boldsymbol s} + \boldsymbol K_{\boldsymbol D}\ldotp \boldsymbol sEn la práctica, en vez de utilizar tres ganancias individuales (Kp , Ki , KD ) se utiliza una única ganancia Kp junto con dos nuevas constantes:
G_c(s) = K_p + K_i\ldotp \frac{1}{s} + K_D\ldotp s\Rightarrow \boldsymbol G_{\boldsymbol c}\left(\boldsymbol s\right) = \boldsymbol K_{\boldsymbol p\ldotp}\left[1 + \frac{1}{\boldsymbol T_{\boldsymbol i}\ldotp \boldsymbol s} + \boldsymbol T_{\boldsymbol D}\ldotp \boldsymbol s\right]Dónde:
\boldsymbol T_{\boldsymbol i} = \frac{\boldsymbol K_{\boldsymbol p}}{\boldsymbol K_{\boldsymbol i}};\ \ \ \ \boldsymbol T_{\boldsymbol D} = \frac{\boldsymbol K_{\boldsymbol D}}{\boldsymbol K_{\boldsymbol p}}Tanto Ti como TD se denominan constantes de tiempo integral y derivativa respectivamente.
En función de las constantes Ti y TD tendremos las siguientes funciones de transferencia para cada acción del controlador PID por separado:
Controlador \ P:\ \ \ \boldsymbol G_{\boldsymbol c}(\boldsymbol s) = \boldsymbol K_{\boldsymbol p}\Rightarrow \ \ \ \ T_i = \infty ;\ T_D = 0Controlador \ PI:\ \ \ \boldsymbol G_{\boldsymbol c}\left(\boldsymbol s\right) = \boldsymbol K_{\boldsymbol p\ldotp}\left[1 + \frac{1}{\boldsymbol T_{\boldsymbol i}\ldotp \boldsymbol s} \right]= \boldsymbol K_{\boldsymbol p}\ldotp \left[\frac{1 + \boldsymbol T_{\boldsymbol i}\ldotp \boldsymbol s}{\boldsymbol T_{\boldsymbol i}\ldotp \boldsymbol s}\right]\Rightarrow \ \ \ \ T_D = 0El controlador PI tiene un polo en el origen y un cero en -1/Ti .
Controlador \ PD:\ \ \ \boldsymbol G_{\boldsymbol c}\left(\boldsymbol s\right) = \boldsymbol K_{\boldsymbol p\ldotp}\left[1 + \boldsymbol T_{\boldsymbol D}\ldotp \boldsymbol s\right]\Rightarrow \ \ \ \ T_i = \infty El controlador PD tiene un cero en -1/TD .
La Función de Transferencia del Controlador PID que incorpora las tres acciones, es:
Controlador \ PID:\ \ \ \boldsymbol G_{\boldsymbol c}\left(\boldsymbol s\right) = \boldsymbol K_{\boldsymbol p\ldotp}\left[1 + \boldsymbol T_{\boldsymbol D}\ldotp \boldsymbol s+\frac{1}{\boldsymbol T_{\boldsymbol i}\boldsymbol s}\right]En algunos casos es preferible expresar la función de transferencia de las acciones del PID de la manera más simple posible:
En función de dos constantes a y b tendremos las siguientes funciones de transferencia para cada acción del controlador PID por separado:
Controlador \ PD:\ \ \ G_c = K(s + a)
Controlador \ PI:\ \ \ G_c = K\frac{(s + b)}{s}Controlador \ PID:\ \ \ G_c = K\frac{(s + a)(s + b)}{s}El uso de los componentes integral y/o derivativo de un Controlador PID tienen implicaciones individuales en cuanto a su desempeño, por lo que sus aplicaciones requieren un buen entendimiento de las bases de estos elementos. Por ello se estudian por separado. Comenzaremos con la porción PD.
Controlador PD. Acción Proporcional – Derivativa
Al añadir un cero, el Controlador PD hace más estable el sistema. La Figura 7 ilustra el comportamiento de una respuesta transitoria antes y después de aplicar un Controlador PD (antes de compensar el sistema mediante una acción Proporcional-Derivativa). En la Figura 7 podemos observar como el Controlador PD mejora el amortiguamiento (reduce la sobreelongación), y produce sistemas más rápidos (reduce el rise-time tr y el settlement-time ts) e incrementa el ancho de banda.
El controlador PD se utiliza principalmente para mejorar la respuesta transitoria de un sistema de control.
La acción del Controlador PD también es conocida como control de velocidad, y su efecto inmediato es que la magnitud de la salida del controlador es proporcional a la velocidad de cambio de la señal de error. El Controlador PD no cambia el Tipo de sistema, es decir, no afecta de forma directa el error en estado estable.
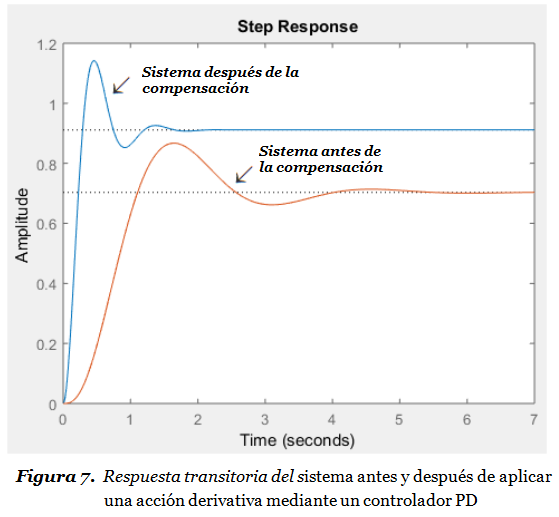
La Figura 7 muestra también que el valor final del sistema compensado está más cerca del valor de referencia (1), por lo tanto el error en estado estable también ha mejorado después de la compensación PD (de 0.297 a 0.088). Sin embargo, los lectores no deben asumir que, en general, la mejora en la respuesta transitoria siempre produce una mejora en el error de estado estable.
La acción de control derivativa D tiene un carácter de previsión. Por sí sola, D responde a la velocidad de cambio del error y produce una corrección significativa antes de que la magnitud del error se vuelva demasiado grande. Debido a que D opera sobre la velocidad de cambio del error y no sobre el error en sí mismo, el controlador D nunca se utiliza solo. Siempre se emplea junto con una acción de control proporcional (PD) o proporcional-integral (PID).
Controlador \ PD:\ \ \ \boldsymbol G_{\boldsymbol c}\left(\boldsymbol s\right) = \boldsymbol K_{\boldsymbol p\ldotp}\left[1 + \boldsymbol T_{\boldsymbol D}\ldotp \boldsymbol s\right]\Rightarrow \ \ \ \ T_i = \infty El controlador PD tiene un cero en -1/TD .
Controlador P. Acción Proporcional
El efecto más inmediato de aplicar un Controlador Proporcional es el desplazamiento de las raíces. El cambio en la ganancia Kp nos permite cambiar el valor de las raíces de la ecuación característica, lo que es lo mismo que cambiar los polos de la función de transferencia a lazo cerrado. La Figura 8 ilustra el comportamiento de una respuesta transitoria antes y después de aplicar un Controlador P (antes de compensar el sistema mediante una acción proporcional).
El efecto más inmediato de aplicar un Controlador Proporcional: el desplazamiento de las raíces. Al cambiar dichos polos, cambiamos el valor del coeficiente de amortiguamiento relativo ζ y la frecuencia natural ωn de una respuesta transitoria ante una entrada escalón unitario, adaptando así dicha respuesta a los requerimientos de diseño.
La acción de control proporcional P además aumenta la ganancia estática del sistema, lo que disminuye el error de estado estable.
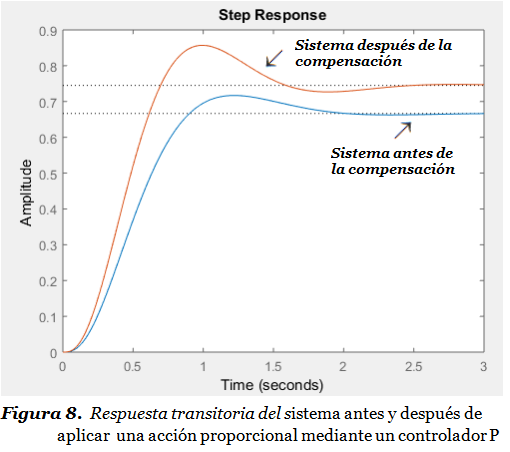
La Figura 8 muestra que efectivamente el error en estado estable es ligeramente más bajo después de la acción de control proporcional, y que el tiempo de levantamiento es menor, pero a costa de un sobrepaso mayor debido a un amortiguamiento menor.
El cambio en la ganancia Kp nos permite cambiar el valor de las raíces de la ecuación característica, disminuye el error de estado estable pero reduce la estabilidad relativa del sistema, aumentando las oscilaciones en la respuesta transitoria.
Controlador \ P:\ \ \ \boldsymbol G_{\boldsymbol c}(\boldsymbol s) = \boldsymbol K_{\boldsymbol p}\Rightarrow \ \ \ \ T_i = \infty ;\ T_D = 0Controlador PI. Acción Proporcional-Integral
Añadir un Controlador PI significa juntar dos ventajas: por un lado obtenemos un amplio margen para cambiar la ubicación de las raíces de la ecuación característica, lo que incide en el amortiguamiento y el tiempo de respuesta de la etapa transitoria, y por otro obtenemos un aumento de la tipología del sistema, lo que significa un mejoramiento en el error en estado estable. La Figura 9 ilustra el comportamiento de una respuesta transitoria antes y después de aplicar un Controlador PI (antes de compensar el sistema mediante una acción Proporcional-Integral).
El error en estado estable de un sistema de control puede ser mejorado directamente, colocando un polo en el origen en el camino de transferencia directa. Pero generalmente conviene lograr esta reducción sin modificar la respuesta transitoria de dicho sistema. Para resolver este problema, además de añadir el polo en el origen, también añadimos un zero cercano a ese polo en el origen. De esta manera mejoramos el error en estado estable sin modificar la respuesta transitoria del sistema. El Controlador PI es el ideal para realizar esta tarea.
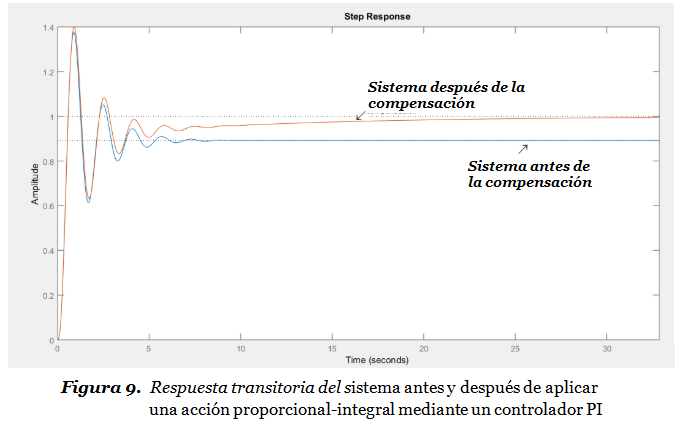
La Figura 9 demuestra que mediante la compensación PI hemos logrado mejorar el error en estado estable sin modificar considerablemente la respuesta transitoria del sistema original. Sin embargo, eligiendo convenientemente los valores de las constantes de Kp y Ti podríamos mejorar la amortiguación (reduciendo el sobreimpulso), aunque esto podría aumentar el tiempo de subida (disminuir el ancho de banda), como sucede en la Figura 10:
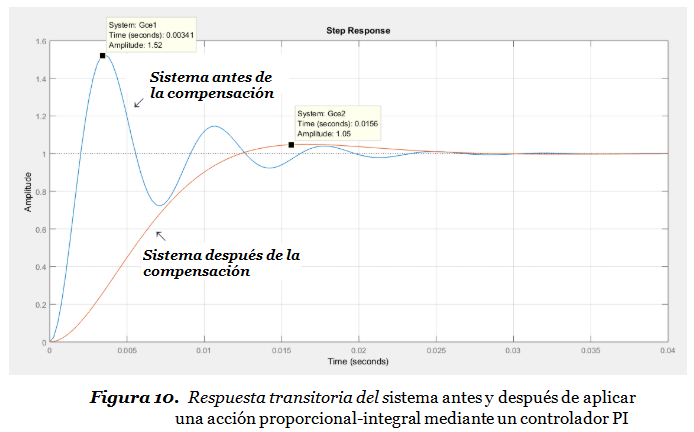
Se pueden elegir diferentes combinaciones de valores para las constantes de Kp y Ti , sólo hay que prestar atención al tema de la estabilidad del sistema.
El Compensador PI tiene un polo en el origen y un zero cerca de dicho polo en el origen, en -1/Ti .
Controlador \ PI:\ \ \ \boldsymbol G_{\boldsymbol c}\left(\boldsymbol s\right) = \boldsymbol K_{\boldsymbol p}\ldotp \left[\frac{1 + \boldsymbol T_{\boldsymbol i}\ldotp \boldsymbol s}{\boldsymbol T_{\boldsymbol i}\ldotp \boldsymbol s}\right]\Rightarrow \ \ \ \ T_D = 0Diseño de Controladores PID
La tarea de diseñar Controladores PID se puede clasificar según las siguientes posibilidades:
- Métodos Empíricos: permiten calcular los valores de los parámetros del PID de manera tal que se satisfagan los requerimientos de diseño, sin contar con un modelo del sistema a controlar:
- Método Ziegler-Nichols en bucle abierto;
- Método Ziegler-Nichols en bucle cerrado.
- Métodos Analíticos: para aplicar estos métodos se necesita de un modelo del sistema a controlar. Permiten obtener los polos deseados del sistema a lazo cerrado, y a partir de allí calcular el valor de los parámetros del PID que satisfagan los requerimientos de diseño:
- Diseño mediante el LGR (Lugar Geométrico de las Raíces);
- Diseño en el dominio de la frecuencia.
Ambos métodos reciben especial atención en la resolución de los siguientes problemas, donde se aplican paso a paso.
Las especificaciones de diseño son el punto de partida en el Diseño de Controladores PID. Utilizando el modelo del sistema, podremos dibujar y utilizar el Lugar Geométrico de las Raíces (LGR) para diseñar el PID de manera tal que cumpla con dichas especificaciones que por lo general están dadas en términos de los valores esperados para los parámetros que describen la respuesta transitoria (Mp , tp, ts y tr) y el error en estado estable. El diseño del Controlador PID por medio del LGR implica seguir los siguientes pasos : Diseño del PID mediante LGR .
Ejercicios resueltos -Controladores PID
PROBLEMA 1.3: Dada la función de transferencia directa G(s) para un sistema de control con realimentación unitaria. Se pretende controlar un sistema motor-reductor para un brazo robótico:
\boldsymbol G(\boldsymbol s) = \frac{1}{\boldsymbol s^2 + 3\boldsymbol s + 2}- Si se busca un tiempo de asentamiento de 0.9 s y un sobrepaso máximo del 5%, ¿Cuál debería ser la posición de los polos dominantes del sistema en el plano complejo?
- Diseñe el regulador PID que consiga cumplir con los requerimientos temporales anteriores.
Encontrarás la solución al Examen 1-1 en el siguiente link: SOLUCIÓN Examen 1-1
Te puede interesar:
- Se resuelven ejercicios de Sistemas de Sistemas de Control, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…
Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos. Al suscribirte podrás contar con excelente material para estudiar y superar con éxito las demandas académicas.
Curso relacionado:
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs
