Ejercicio S2O-1. Parámetros del Sistema de Segundo Orden. -

Ejercicio resuelto para profundizar en la comprensión de Sistemas de Segundo Orden Subamortiguados.

Ejercicio S2O-1: Considere el sistema S1 de segundo orden subamortiguado cuya FT es G(s), ecuación (1):

\boldsymbol G(\boldsymbol s) = \frac{22}{\boldsymbol s^2 + 2\boldsymbol s + 22};\ \ \ (1)

Realizar los siguientes pasos:

Determinar la expresión matemática estándar de los polos de un sistema de segundo orden.
Calcular el valor de La Ganancia Estática K , El Coeficiente de Amortiguamiento ζ y La Frecuencia Natural ω_n para el sistema s1.
En base al paso anterior, ¿Cuáles son los polos del sistema S1? Comprobar en Matlab los resultados anteriores. Graficar la salida de S1 ante una entrada escalón unitario. ¿Se comporta como un sistema subamortiguado?
Determinar la expresión matemática de la salida en el tiempo de un sistema de segundo orden ante una entrada escalón unitario.
Hacer análisis matemático de los parámetros más importantes del sistema subamortiguado ante una entrada escalón unitario: tiempo de estabilización, tiempo de subida, tiempo pico, sobreoscilación. Utilizar la simulación del paso anterior para comprobar en Matlab el valor de cada parámetro.
Determinar la expresión matemática de la salida de un sistema de segundo orden ante una entrada impulso (Respuesta impulsiva).
Graficar la respuesta impulsiva del sistema S1.

Lo polos de un sistema de segundo orden.

Para determinar la expresión matemática de los polos de un sistema de segundo orden utilizamos La Función de Transferencia Estándar:

\boldsymbol G(\boldsymbol s) = \frac{\boldsymbol K\boldsymbol \omega_{\boldsymbol n}^2}{\boldsymbol s^2 + 2\boldsymbol \zeta \boldsymbol \omega_{\boldsymbol n}\boldsymbol s + \boldsymbol \omega_{\boldsymbol n}^2}

\boldsymbol K: Ganancia \ Estática;\ \ \ \ \boldsymbol \omega_{\boldsymbol n}:Frecuencia\ natural\ no\ amortiguada

\boldsymbol \zeta: Coeficiente\ o\ Factor\ de\ Amortiguamiento

Los polos son aquellos valores de “s” para los cuáles el denominador de la ecuación (2) se hace cero. Es decir:

\boldsymbol s^2 + 2\boldsymbol \zeta \boldsymbol \omega_{\boldsymbol n}\boldsymbol s + \boldsymbol \omega_{\boldsymbol n}^2=0

Resolvemos convenientemente la ecuación anterior:

s = - \zeta \omega_n \pm \sqrt{\zeta^2\omega_n^2 - \omega_n^2}

s = - \zeta \omega_n \pm \omega_n\sqrt{( - 1)(1 - \zeta^2)}

\boldsymbol s = - \boldsymbol \zeta \boldsymbol \omega_{\boldsymbol n} \pm \boldsymbol j\boldsymbol \omega_{\boldsymbol n}\sqrt{1 - \boldsymbol \zeta^2}

A partir de los anteriores se definen además los siguientes parámetros para un Sistema de Segundo Orden:

\boldsymbol \sigma = \boldsymbol \zeta \boldsymbol \omega_{\boldsymbol n}:\ Factor\ de\ Crecimiento\ ó\ Constante\ de \ Atenuación

\boldsymbol \omega_{\boldsymbol d} = \boldsymbol \omega_{\boldsymbol n}\sqrt{1 - \boldsymbol \zeta^2}:\ Frecuencia\ Natural\ Amortiguada

Por cuestiones prácticas nos conviene expresar los polos del sistema de segundo orden en términos de σ y ω_d :

\boldsymbol s = - \boldsymbol \sigma \pm \boldsymbol j\boldsymbol \omega_{\boldsymbol d}\ \ \ (3)

¿Cuáles son los polos del sistema S1?

Utilizando la FT del sistema S1 e igualando las ecuaciones (1) y (2) vemos que:

\boldsymbol G(\boldsymbol s) =\frac{\boldsymbol K\boldsymbol \omega_{\boldsymbol n}^2}{\boldsymbol s^2 + 2\boldsymbol \zeta \boldsymbol \omega_{\boldsymbol n}\boldsymbol s + \boldsymbol \omega_{\boldsymbol n}^2}= \frac{22}{\boldsymbol s^2 + 2\boldsymbol s + 22}

\boldsymbol \omega_{\boldsymbol n}^2 = 22\rightarrow \boldsymbol \omega_{\boldsymbol n} = 4.69

\boldsymbol \zeta \boldsymbol \omega_{\boldsymbol n} = 1\rightarrow \boldsymbol \zeta = \frac{1}{\boldsymbol \omega_{\boldsymbol n}} = 0.213

Por lo tanto:

\boldsymbol \sigma = \boldsymbol \zeta \boldsymbol \omega_{\boldsymbol n}=1

\boldsymbol \omega_{\boldsymbol d} = \boldsymbol \omega_{\boldsymbol n}\sqrt{1 - \boldsymbol \zeta^2}=4.58

Utilizando la ecuación (3), los polos del sistema S1 son:

\boldsymbol s_1 = - 1 + \boldsymbol j4.58

\boldsymbol s_2 = - 1 - \boldsymbol j4.58

Se confirman que se trata de dos polos complejos conjugados con la parte real negativa. El sistema S1 se comporta como un sistema subamortiguado ante una entrada escalón unitario. La siguiente simulación lo comprueba.

Grafica de la salida del sistema S1 ante una entrada escalón unitario

Desarrollamos el siguiente script en la consola de Matlab con el fin de graficar la respuesta del sistema S1 a la entrada escalón unitario:

>> S1=tf([22],[1 2 22])

S1 =
 
        22
  --------------
  s^2 + 2 s + 22
 
Continuous-time transfer function.
Model Properties
>> step(S1)
>> title('Respuesta del sistema S1 al escalon unitario')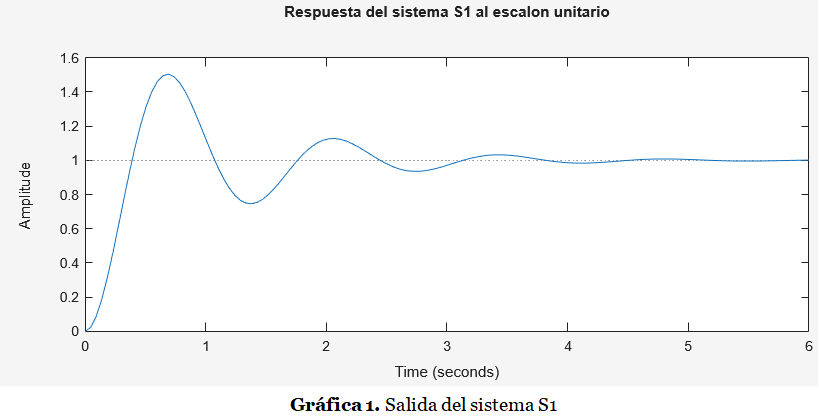

El siguiente comando en la consola de Matlab nos da la ubicación de los polos del sistema S1, además de que nos confirma el valor calculado para la Frecuencia natural y para el Factor de Amortiguamiento (Damping):

>> damp(S1)
                                                                       
         Pole              Damping       Frequency      Time Constant  
                                       (rad/seconds)      (seconds)    
                                                                       
 -1.00e+00 + 4.58e+00i     2.13e-01       4.69e+00         1.00e+00    
 -1.00e+00 - 4.58e+00i     2.13e-01       4.69e+00         1.00e+00

Salida en el tiempo de un sistema de 2do. Orden ante una entrada escalón unitario.

Para determinar la expresión matemática de la respuesta de un sistema de segundo orden a una entrada escalón unitario, utilizamos nuevamente La Función de Transferencia Estándar para un sistema cuya entrada es x(t) y cuya salida es y(t) :

\boldsymbol G(\boldsymbol s) =\frac{\boldsymbol Y(\boldsymbol s)}{\boldsymbol X(\boldsymbol s)}= \frac{\boldsymbol K\boldsymbol \omega_{\boldsymbol n}^2}{\boldsymbol s^2 + 2\boldsymbol \zeta \boldsymbol \omega_{\boldsymbol n}\boldsymbol s + \boldsymbol \omega_{\boldsymbol n}^2};

La transformada de Laplace de una entrada x(t) escalón unitario es:

\boldsymbol X(\boldsymbol s) = \frac{1}{\boldsymbol s}

Por lo tanto, la transformada de Laplace de la salida del sistema para una entrada escalón unitario es:

\boldsymbol Y(\boldsymbol s) = \frac{\boldsymbol K\boldsymbol \omega_{\boldsymbol n}^2}{\boldsymbol s^2 + 2\boldsymbol \zeta \boldsymbol \omega_{\boldsymbol n}\boldsymbol s + \boldsymbol \omega_{\boldsymbol n}^2} \times \frac{1}{\boldsymbol s}

La expresión matemática para y(t) se logra aplicando la antitransformada de Laplace a Y(s) :

y(t) = {\mathcal{L}}^{- 1}\left\{\boldsymbol Y(\boldsymbol s)\right\} = {\mathcal{L}}^{- 1}\left\{\frac{k\omega_n^2}{s(s^2 + 2\zeta \omega_ns + \omega_n^2)}\right\}

En definitiva, la expresión matemática de la respuesta y(t) de un sistema de segundo orden a una entrada escalón unitario es:

\boldsymbol y(\boldsymbol t) = \boldsymbol k(1 - \frac{\boldsymbol e^{- \boldsymbol \zeta \boldsymbol \omega_{\boldsymbol n}\boldsymbol t}}{\sqrt{1 - \boldsymbol \zeta^2}}\boldsymbol s\boldsymbol e\boldsymbol n(\boldsymbol \omega_{\boldsymbol d}\boldsymbol t - \boldsymbol \theta ))

Dónde:

\boldsymbol \zeta = \mathbf c\mathbf o\mathbf s(\boldsymbol \theta );\ \ 0 \leq \zeta < 1;\ \ \ t \geq 0;\ \ \ \omega_{\boldsymbol d}=\omega_{\boldsymbol n}\sqrt{1 - \boldsymbol \zeta^2}

Parámetros del sistema subamortiguado

Para calcular el valor de los parámetros para el sistema subamortiguado S1, utilizamos las fórmulas presentadas en la teoría:

Tiempo de asentamiento:

t_s \approx \frac{\pi }{\sigma } = \frac{\pi }{1}

Settling \ time:\ \ \boldsymbol t_{\boldsymbol s} \approx 3.14\ \boldsymbol s

Tiempo de subida:

t_r \approx \frac{\pi - \theta }{\omega_d}\Rightarrow \theta = cos^{- 1}(\zeta ) = {\mathrm{\cos }}^{- 1}\left(0.213\right) = 77.7 \times \pi / 180 = 1.356

t_r \approx \frac{3.142 - 1.356}{4.58}

Rise\ time:\ \ \boldsymbol t_{\boldsymbol r} \approx 0.39\ \boldsymbol s

Tiempo Pico:

t_p = \frac{\pi }{\omega_d} = \frac{\pi }{4.58}

Peak\ time:\ \ \boldsymbol t_{\boldsymbol p} = 0.686\ \boldsymbol s

Sobrepaso Máximo:

M_p = e^{- \frac{\zeta \pi }{\sqrt{1 - \zeta^2}}} = e^{- \frac{(0.213)\pi }{\sqrt{1 - (0.213)^2}}} = e^{- 0.685}

Overshooting:\ \ \boldsymbol M_{\boldsymbol p} = 0.5

\% \boldsymbol M_{\boldsymbol p} = 50\%

Para corroborar estos resultados desarrollamos el siguiente script en la consola de Matlab:

>> S1=tf([22],[1 2 22]);
>> stepinfo(S1)

ans = 

  struct with fields:

         RiseTime: 0.2608
    TransientTime: 3.6352
     SettlingTime: 3.6352
      SettlingMin: 0.7465
      SettlingMax: 1.5037
        Overshoot: 50.3661
       Undershoot: 0
             Peak: 1.5037
         PeakTime: 0.6908

Comentarios: "Comparamos lo obtenido en nuestro análisis con los resultados en Matlab:
* Tiempo de asentamiento: 3.14 s contra 3.63 s(por eso utilizamos el símbolo "aproximadamente" en los cálculos)
* Tiempo de subida: 0.39 s contra 0.26 s (aquí Matlab utiliza sin duda una fórmula distinta ya que en la Gráfica este tiempo coincide con una amplitud de 0.5 más o menos)
* Tiempo Pico: 0.68 s contra 0.69 s (coincide)
* Sobrepaso Máximo: 50% contra 50%(coincide)

En la Gráfica 2 podemos ver algunos datos aproximados sobre los parámetros calculados:

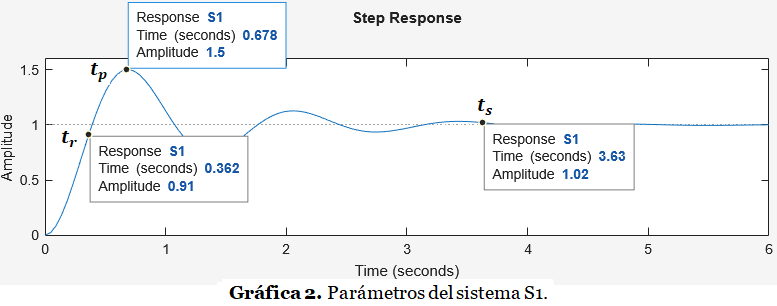
Respuesta Impulsiva – Salida en el tiempo ante una entrada impulso.

Para determinar la expresión matemática de la respuesta impulsiva de un sistema de segundo orden, utilizamos La Función de Transferencia Estándar para un sistema cuya entrada es x(t) y cuya salida es y(t) :

\boldsymbol G(\boldsymbol s) =\frac{\boldsymbol Y(\boldsymbol s)}{\boldsymbol X(\boldsymbol s)}= \frac{\boldsymbol K\boldsymbol \omega_{\boldsymbol n}^2}{\boldsymbol s^2 + 2\boldsymbol \zeta \boldsymbol \omega_{\boldsymbol n}\boldsymbol s + \boldsymbol \omega_{\boldsymbol n}^2};

La transformada de Laplace de una entrada x(t) impulso es:

\boldsymbol X(\boldsymbol s) = 1

Por lo tanto, la transformada de Laplace de la salida del sistema para una entrada impulso es:

\boldsymbol Y(\boldsymbol s) = \frac{\boldsymbol K\boldsymbol \omega_{\boldsymbol n}^2}{\boldsymbol s^2 + 2\boldsymbol \zeta \boldsymbol \omega_{\boldsymbol n}\boldsymbol s + \boldsymbol \omega_{\boldsymbol n}^2} \times1

La expresión matemática para y(t) se logra aplicando la antitransformada de Laplace a Y(s) :

y(t) = {\mathcal{L}}^{- 1}\left\{\boldsymbol Y(\boldsymbol s)\right\} = {\mathcal{L}}^{- 1}\left\{\frac{k\omega_n^2}{s^2 + 2\zeta \omega_ns + \omega_n^2}\right\}

En definitiva, la expresión matemática de la respuesta y(t) de un sistema de segundo orden a una entrada impulso unitario es:

\boldsymbol y(\boldsymbol t) = \frac{\boldsymbol \omega_{\boldsymbol n}}{\sqrt{1 - \boldsymbol \zeta^2}}\boldsymbol e^{- \boldsymbol \zeta \boldsymbol \omega_{\boldsymbol \eta}\boldsymbol t}\boldsymbol s\boldsymbol e\boldsymbol n(\boldsymbol \omega_{\boldsymbol d}t)

Dónde:

0 \leq \zeta < 1;\ \ \ t \geq 0;\ \ \ \omega_{\boldsymbol d}=\omega_{\boldsymbol n}\sqrt{1 - \boldsymbol \zeta^2}

La respuesta impulsiva también se puede obtener derivando al respuesta al escalón unitario, ya que la función impulso unitario es la derivada en el tiempo de la función escalón unitario.

Gráfica de la respuesta impulsiva del sistema S1

Desarrollamos el siguiente script en la consola de Matlab con el fin de graficar la respuesta impulsiva del sistema S1 :

>> S1=tf([22],[1 2 22]);
>> impulse(S1)
>> title('Respuesta impulsiva del sistema S1')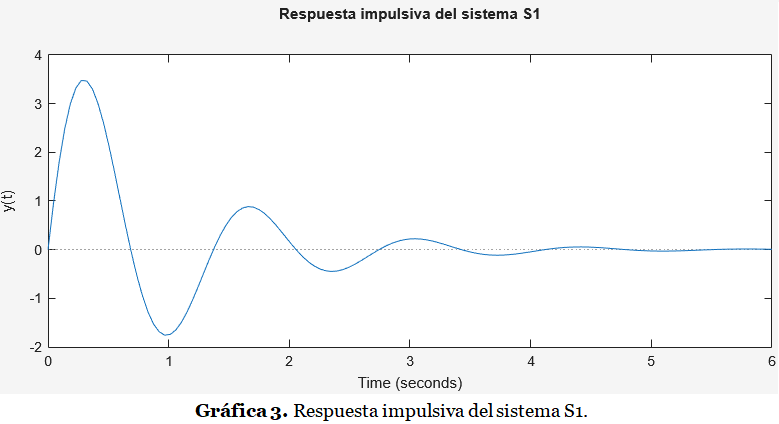

Es interesante notar que la forma de la curva de la Gráfica 3 es la misma foma de la curva de la respuesta y(t) a la entrada impulso, y que esta respuesta caracteriza completamente el sistema, lo que significa que posee toda la información necesaria sobre el sistema para hallar la salida ante cualquier entrada a través del proceso de convolución. Por esto, a la respuesta y(t) a la entrada impulso se le da con frecuencia en el análisis de sistemas la notación de h(t) .

Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos.

Te puede interesar:

Se resuelven ejercicios de Sistemas de Primer y Segundo Orden, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…

Curso relacionado:

Sistemas de Control 1

Señales y Sistemas 1