Considerando el Sistema de Control más genérico posible, Figura adjunta, El Lugar Geométrico de Las Raíces (LGR) es un procedimiento que nos permite observar en un gráfico la trayectoria de desplazamiento en el plano “s” de los polos de dicho sistema a lazo cerrado (la trayectoria de las raíces del polinomio característico sin tener que calcular el valor numérico de todas ellas) a medida que varía el valor de un parámetro a lazo abierto (generalmente la ganancia K). El LGR proporciona valiosa información para evaluar la estabilidad del sistema y para diseñar una respuesta transitoria del mismo que cumpla con ciertos requerimientos, eligiendo un rango de valores deseables para K.
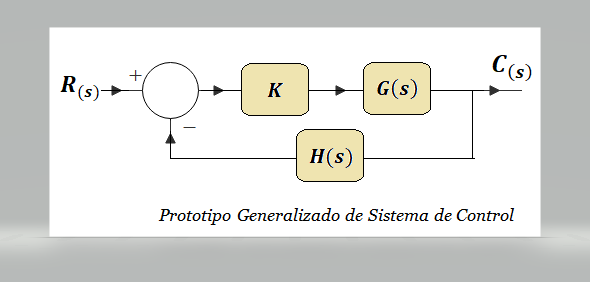
El Lugar Geométrico de las Raíces – Definición
La Figura 1 muestra el sistema de control prototipo más simple y generalizado que podamos concebir:
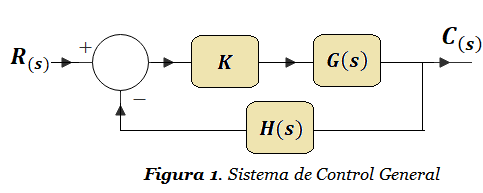
La Función de Transferencia a lazo cerrado de la Figura 1 es:
\frac{\boldsymbol C(\boldsymbol s)}{\boldsymbol R(\boldsymbol s)} = \boldsymbol K\frac{\boldsymbol G(\boldsymbol s)}{1 + \boldsymbol K\boldsymbol G(\boldsymbol s)\boldsymbol H(\boldsymbol s)}\ \ \ \ (1)Ya vimos en Función de Transferencia que las propiedades fundamentales de la respuesta en el tiempo de un sistema de control como el de la Figura 1 dependen de la ubicación de las raíces del Polinomio Característico en el plano complejo, raíces llamadas “polos” del sistema (en lazo cerrado).
De la ecuación (1) extraemos El Polinomio Característico p(s) (ó ecuación característica) del sistema genérico de la Figura 1 :
Polinomio Característico:
\boldsymbol p(\boldsymbol s) = \boldsymbol 1 + \boldsymbol K\boldsymbol G(\boldsymbol s)\boldsymbol H(\boldsymbol s)\ \ \ \ (2)
En (2) el factor G(s)H(s) constituye La Función de Transferencia en lazo abierto del sistema de la Figura 1. Para hallar los polos del sistema simplemente igualamos (2) a cero:
\boldsymbol p(\boldsymbol s) = \boldsymbol 1 + \boldsymbol K\boldsymbol G(\boldsymbol s)\boldsymbol H(\boldsymbol s)=0\ \ \ \ (3)
La ecuación (3) se conoce como La Ecuación Característica, de dónde se deduce que los polos del sistema estarán ubicados en aquellos valores de “s” para los cuáles:
\boldsymbol K\boldsymbol G(\boldsymbol s)\boldsymbol H(\boldsymbol s) = - 1\ \ \ \ (4)
La idea básica detrás del método LGR es que los valores de “s” que hacen que el factor KG(s)H(s)= -1 satisfacen dos condiciones simultáneamente: El Criterio del Ángulo y El Criterio del Módulo. Tomando en cuenta (3) y (4):
G\left(s\right)H\left(s\right) = - \frac{1}{K}El Criterio del Módulo:
\left|\boldsymbol G\left(\boldsymbol s\right)\boldsymbol H\left(\boldsymbol s\right)\right| = \frac{1}{\boldsymbol K}El Criterio del Ángulo:
\angle \boldsymbol G\left(\boldsymbol s\right)\boldsymbol H\left(\boldsymbol s\right) = 180\degree + \boldsymbol q\ldotp 360\degree \boldsymbol s\boldsymbol i\ \ \boldsymbol K > 0,\ \boldsymbol p\boldsymbol a\boldsymbol r\boldsymbol a\ \ \boldsymbol q = 0,1,2,\ldotp \ldotp \ldotp
\angle \boldsymbol G\left(\boldsymbol s\right)\boldsymbol H\left(\boldsymbol s\right) = \boldsymbol q\ldotp 360\degree \boldsymbol s\boldsymbol i\ \boldsymbol K < 0,
Los valores de “s” que satisfacen El Criterio del Ángulo y El Criterio del Módulo son las raíces de la ecuación característica, es decir, los polos en lazo cerrado, «El lugar geométrico de las raíces es una gráfica de los puntos en el plano complejo que satisfacen únicamente la condición de ángulo. Las raíces de la ecuación característica (los polos de lazo cerrado) que corresponden a un valor específico de la ganancia se determinan a partir de la condición de magnitud.» (Ogata, Ingeniería de Control, p319).
Una de las ventajas de trabajar con el LGR se observa en los criterios del Ángulo y del Módulo: el método se enfoca en los polos y ceros de la Función de Transferencia (FT) a lazo abierto, la cual suele ser más sencilla que la FT a lazo cerrado.
Para pintar el LGR en función del controlador proporcional de ganancia K:
- Se calculan los polos y los ceros de la función de transferencia a lazo abierto y se localizan en el plano complejo;
- El LGR será un conjunto de líneas simétricas respecto al eje real que parten de los polos en lazo abierto y terminan en los ceros a lazo abierto;
- Si el número de polos y ceros no coinciden, algunas ramas van hacia el infinito;
- El LGR trazado nos permite entender con más profundidad la importancia de los polos y los ceros del sistema realimentado;
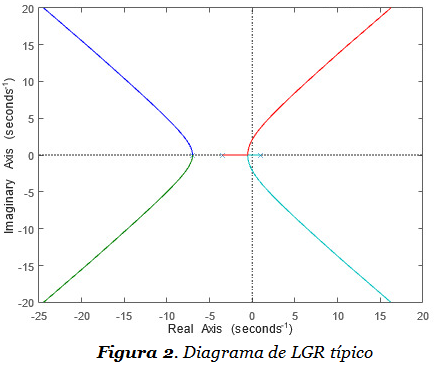
- Podemos dibujar aproximadamente el LGR mediante las siguientes reglas. El dibujo exacto del LGR nos lo puede proporcionar Matlab (Figura 2).
Reglas para el trazado del LGR
\boldsymbol G(\boldsymbol s)\boldsymbol H(\boldsymbol s): FT\ a\ lazo\ abierto
\boldsymbol 1 + \boldsymbol K\boldsymbol G(\boldsymbol s)\boldsymbol H(\boldsymbol s)=0:\ ecuación \ característica
Las 7 reglas que se dan a continuación se basan en la relación entre los polos y ceros de G(s).H(s) (lazo abierto) y las raíces de La Ecuación Característica del sistema en lazo cerrado (polos en lazo cerrado), siendo K el parámetro variable.
1era. Regla. Identificar y ubicar los polos y ceros en lazo abierto.
Lo primero que debemos hacer es obtener la ecuación característica. Luego, expresar en forma factorizada la función G(s)H(s).
Dibujamos el plano complejo (o plano «s») y localizamos los polos (con cruces) y ceros (con círculos) de G(s)H(s) en dicho plano:
\boldsymbol G(\boldsymbol s)\boldsymbol H(\boldsymbol s) = \boldsymbol K\frac{\boldsymbol B(\boldsymbol s)}{\boldsymbol A(\boldsymbol s)} = \boldsymbol K\frac{(\boldsymbol s + \boldsymbol z_1)\left(\boldsymbol s + \boldsymbol z_2\right)\ldotp \ldotp \ldotp \left(\boldsymbol s + \boldsymbol z_{\boldsymbol m}\right)}{\left(\boldsymbol s + \boldsymbol p_1\right)\left(\boldsymbol s + \boldsymbol p_2\right)\ldotp \ldotp \ldotp \left(\boldsymbol s + \boldsymbol p_{\boldsymbol n}\right)}\ \ \ \ (5)El objetivo es aislar a K como factor multiplicativo de la función B(s)/A(s). En este análisis suponemos que la ganancia K es el parámetro de interés. El método es aplicable sin embargo, a sistemas con parámetros de interés diferentes a la ganancia.
Si expresamos La ecuación característica (2) en términos de la ecuación (5) obtenemos:
1+ \boldsymbol K\frac{(\boldsymbol s + \boldsymbol z_1)\left(\boldsymbol s + \boldsymbol z_2\right)\ldotp \ldotp \ldotp \left(\boldsymbol s + \boldsymbol z_{\boldsymbol m}\right)}{\left(\boldsymbol s + \boldsymbol p_1\right)\left(\boldsymbol s + \boldsymbol p_2\right)\ldotp \ldotp \ldotp \left(\boldsymbol s + \boldsymbol p_{\boldsymbol n}\right)}=0\ \ \ \ (6)La ecuación 6 demuestra que «Los lugares geométricos de las raíces son los lugares geométricos de los polos en lazo cerrado conforme la ganancia K varía de cero a infinito» (Ogata, Ingeniería de Control, p320).
2da. Regla. Determinar el número de ramas.
El número de ramas es igual al mayor número de polos o de ceros de la función G(s)H(s) (o GH por economía de espacio).
En (5) el número de ramas es igual a m si m>n, o es igual a n si n>m :
\boldsymbol N\boldsymbol ú\boldsymbol m\boldsymbol e\boldsymbol r\boldsymbol o\ de\ ramas = max\ \{ nº\ de\ polos\ de\ GH,nº\ de\ ceros\ de\ GH\} - Las ramas del LGR inician en los polos de GH y terminan en los ceros de GH ;
- El LGR es simétrico respecto al eje real del plano s.
3ra. Regla. Identificar los segmentos en el eje real.
Debido a la simetría conjugada de los lugares geométricos de las raíces, los puntos de desprendimiento y de ingreso se encuentran sobre el eje real o bien ocurren en pares complejos conjugados. Al dibujar sobre el eje real, debemos seleccionar un punto en éste. Si la cantidad total de polos y ceros reales a la derecha de este punto de prueba es impar, este punto se encuentra en el lugar geométrico de las raíces. Si en cambio esta cantidad es par, entonces este punto no pertenece al lugar geométrico de las raíces. Todos los puntos del plano real que pertenecen al LGR forman una sección, un rango de valores que se resalta mediante una línea. En esta sección, K es mayor o igual a cero.
Los Tramos del eje real que pertenecen al LGR son aquellos que dejan a su derecha un número impar de polos + ceros.
4ta. Regla. Calcular las asíntotas.
Algunos de los lugares geométricos se aproximan al infinito cuando n y m de (5) no son iguales. Las propiedades del lugar geométrico de las raíces cerca del infinito en el plano s se describen mediante las asíntotas del lugar geométrico cuando s se hace muy grande.
Esta regla contempla tres pasos:
- Calcular el número de asíntotas:
número \ de\ asíntotas=\boldsymbol n - \boldsymbol m
- Calcular el ángulo θ de cada asíntota con el eje real:
\boldsymbol \theta_{\boldsymbol a\mathbf s\mathbf i\mathbf n\boldsymbol t\boldsymbol o\boldsymbol t\boldsymbol a} = \frac{180\degree \ldotp (2\boldsymbol q + 1)}{\boldsymbol n - \boldsymbol m}\boldsymbol ;\ \ \ \ para\ q = 0,1,2,\ldotp \ldotp \ldotp ,(n - m) - 1- Calcular el centroide σ (punto intersección de las n-m asíntotas con el eje real):
\boldsymbol \sigma = \frac{\sum_{\boldsymbol j = 1}^{\boldsymbol n}\boldsymbol p\boldsymbol o\boldsymbol l\boldsymbol o_{\boldsymbol j} - \sum_{\mathbf i = 1}^{\boldsymbol m}\boldsymbol c\boldsymbol e\boldsymbol r\boldsymbol o_{\boldsymbol i}}{\boldsymbol n - \boldsymbol m}5ta. Regla. Identificar los puntos de corte con el eje imaginario.
Los puntos en donde los lugares geométricos de las raíces interceptan el eje jω se encuentran con facilidad por medio del criterio de estabilidad de Routh-Hurwitz aplicado a la ecuación característica.
Esta regla contempla cuatro pasos:
- Construir la Tabla de Routh en función de la ganancia K
- Igualar a cero el término o fila correspondiente a s1, despejar el valor de K de la ecuación resultante y etiquetarla como ganancia crítica.
- Sustituir el valor de la ganancia crítica en la tabla, determinar el valor de la constante de la fila correspondiente a s2, utilizando las reglas clásicas de la tabla de Routh.
- Sustituir el valor de las constantes anteriores en la fila correspondiente a s2 e igualarla a cero. Obtener las raíces del polinomio de segundo grado resultante. Este procedimiento arroja dos valores para «s», obteniendo así los puntos de corte con el eje imaginario. Recordar que s=jω en el eje de las ordenadas y así podemos conocer el valor de ω.
6ta. Regla. Determinar los puntos de ruptura con el eje real.
Esta regla trata sobre el caso en que dos ramas del LGR se encuentran en un punto de quiebre en el eje real y luego se ramifican desde este eje en direcciones opuestas. En este caso, el punto de quiebre representa una raíz doble de la ecuación 1+KG(s)H(s)=0, cuando se le asigna el valor K apropiado. También se presenta el caso en donde dos lugares de las raíces polares conjugadas complejas se aproximan al eje real, se encuentran en un punto de quiebre y luego se ramifican en direcciones opuestas a lo largo del eje real. En general, un punto de quiebre puede involucrar más de dos lugares de las raíces.
Todos los puntos de ruptura deben satisfacer las ecuaciones siguientes, pero no todas las soluciones de estas ecuaciones son puntos de ruptura.
\frac{\boldsymbol d\boldsymbol G(\boldsymbol s)\boldsymbol H(\boldsymbol s)}{\boldsymbol d\boldsymbol s} = 0- La igualdad anterior implica determinar la expresión para G(s)H(s) , obtener su derivada con respecto a «s», igualarla a cero y resolver para «s» (encontrar sus raíces).
\frac{\boldsymbol d\boldsymbol K(\boldsymbol s)}{\boldsymbol d\boldsymbol s} = 0- La igualdad anterior implica despejar la constante K en función de «s», obtener su derivada con respecto a «s», igualarla a cero y resolver para «s» (encontrar sus raíces).
- Ambos puntos, el centroide y el punto de rutptura, suelen estar cercanos y algunas veces coinciden.
7ma. Regla. Determinar los ángulos de salida y de llegada de las raíces del LGR.
Para trazar los lugares geométricos de las raíces con una precisión razonable, debemos encontrar las direcciones de los lugares de las raíces cerca de los polos y ceros complejos. El ángulo de partida de un polo o de llegada al cero, de un lugar geométrico de las raíces de G(s)H(s), denota el ángulo tangente del lugar geométrico cerca del punto de partida o de llegada.
Para calcular el ángulo de salida del polo p1 (un polo complejo conjugado cualquiera), se selecciona un punto de prueba s1 cercano a p1 , y se aplica la siguiente fórmula:
- El ángulo de salida de un polo complejo p1 es igual a 180 grados más la suma de los ángulos vectoriales hacia el polo complejo s1 , desde los otros ceros, menos la suma de los ángulos vectoriales hacia el polo complejo s1 , desde los otros polos.
\boldsymbol Á\boldsymbol n\boldsymbol g\boldsymbol u\boldsymbol l\boldsymbol o\ \boldsymbol d\boldsymbol e\ \boldsymbol s\boldsymbol a\boldsymbol l\boldsymbol i\boldsymbol d\boldsymbol a_{\ \boldsymbol p\boldsymbol o\boldsymbol l\boldsymbol o\ \boldsymbol p_1} = 180\degree + \left(\sum \measuredangle \mathbf c\mathbf e\mathbf r\boldsymbol o\boldsymbol s_{\boldsymbol s_1}\right) - \left(\sum \measuredangle \boldsymbol p\boldsymbol o\boldsymbol l\boldsymbol o\boldsymbol s_{\boldsymbol s_1}\right)Elegimos un punto s1 cercano al polo complejo p1. Aplicamos el criterio de fase (la fase total de G(s)H(s) es igual a 180º) y resolvemos. Desde un polo complejo cualquiera, el ángulo de salida es la diferencia entre el ángulo total debido a los demás polos y ceros y el ángulo del criterio: 180º+q.360º
Observación: Los ángulos de las variables complejas sobre el LGR y que inician en los polos y ceros en lazo abierto, se miden en sentido contrario a las manecillas del reloj.
Para calcular el ángulo de llegada a un cero complejo c1 utilizamos la siguiente fórmula:
\boldsymbol Á\boldsymbol n\boldsymbol g\boldsymbol u\boldsymbol l\boldsymbol o\ \boldsymbol d\boldsymbol e\ \boldsymbol l\boldsymbol l\boldsymbol e\boldsymbol g\boldsymbol a \boldsymbol d\boldsymbol a_{\ \boldsymbol c\boldsymbol e\boldsymbol r\boldsymbol o\ \boldsymbol c_1} = 180\degree - \left(\sum \measuredangle \mathbf c\mathbf e\mathbf r\boldsymbol o\boldsymbol s_{\boldsymbol s_1}\right) + \left(\sum \measuredangle \boldsymbol p\boldsymbol o\boldsymbol l\boldsymbol o\boldsymbol s_{\boldsymbol s_1}\right)Los sistemas de control realimentados son difíciles de comprender desde el punto de vista cualitativo, por lo que dicha comprensión depende en gran medida de las matemáticas. El Lugar Geométrico de las Raíces es la técnica gráfica que nos da esa descripción cualitativa sobre el rendimiento del sistema de control que estamos diseñando.
Te puede interesar:
- Se resuelven ejercicios de Señales y Sistemas, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…
Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos. Al suscribirte podrás contar con excelente material para estudiar y superar con éxito las demandas académicas.
Curso relacionado:
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs
