Función de Transferencia S. MRA – Ejercicio resuelto 6 -

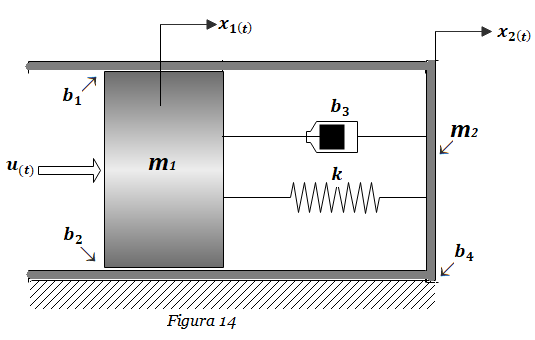
Ejercicio FT-6: Obtener la Función de Transferencia H_1(s)=X_1(s)/U_(s) y H_2(s)=X_2(s)/U_(s) del sistema masa-resorte-amortiguador de la Figura 14.

Obtención de la ecuación del sistema. Dinámica del sistema.

Las fuerzas que intervienen en el movimiento (o dinámica) del sistema son las siguientes:

Paso 1. Identificar todas las fuerzas que intervienen en el sistema (utilizar diagrama de cuerpo libre puede ayudar a identificar dichas fuerzas). Simultáneamente, expresar matemáticamente dichas fuerzas utilizando las leyes de la física.

La fuerza F_resorte se calcula mediante la Ley de Hooke. Por inercia, la masa m se opone a cambiar su estado de movimiento mediante una F_masa.

La constante de fricción viscosa b genera la fuerza F_amortiguador. La fuerza de roce con el piso es nula. La fuerza externa F_externa se ejerce directamente sobre la masa m₁ , y es denominada u(t) en el esquema mecánico.

Las unidades utilizadas son: x: desplazamiento (m) ; t: tiempo (s); k: constante de elasticidad (N/m); m: unidad de masa. (N-s²/m)

b: constante de fricción viscosa. (N-s/m); u(t): Fuerza (N)

\boldsymbol F_{\boldsymbol r\boldsymbol e\boldsymbol s\boldsymbol o\boldsymbol r\boldsymbol t\boldsymbol e1.1} = \boldsymbol k\boldsymbol x_1(\boldsymbol t)

\boldsymbol F_{\boldsymbol r\boldsymbol e\boldsymbol s\boldsymbol o\boldsymbol r\boldsymbol t\boldsymbol e1.2} = \boldsymbol k\boldsymbol x_2(\boldsymbol t)

\boldsymbol F_{\boldsymbol a\boldsymbol m\boldsymbol o\boldsymbol r\boldsymbol t\boldsymbol i\boldsymbol g\boldsymbol u\boldsymbol a\boldsymbol d\boldsymbol o\boldsymbol r 1} = \boldsymbol b_1\frac{\boldsymbol d\boldsymbol x_1(\boldsymbol t)}{\boldsymbol d\boldsymbol t}

\boldsymbol F_{\boldsymbol a\boldsymbol m\boldsymbol o\boldsymbol r\boldsymbol t\boldsymbol i\boldsymbol g\boldsymbol u\boldsymbol a\boldsymbol d\boldsymbol o\boldsymbol r 2} = \boldsymbol b_2\frac{\boldsymbol d\boldsymbol x_1(\boldsymbol t)}{\boldsymbol d\boldsymbol t}

\boldsymbol F_{\boldsymbol a\boldsymbol m\boldsymbol o\boldsymbol r\boldsymbol t\boldsymbol i\boldsymbol g\boldsymbol u\boldsymbol a\boldsymbol d\boldsymbol o\boldsymbol r 3.1} = \boldsymbol b_3\frac{\boldsymbol d\boldsymbol x_1(\boldsymbol t)}{\boldsymbol d\boldsymbol t}

\boldsymbol F_{\boldsymbol a\boldsymbol m\boldsymbol o\boldsymbol r\boldsymbol t\boldsymbol i\boldsymbol g\boldsymbol u\boldsymbol a\boldsymbol d\boldsymbol o\boldsymbol r 3.2} = \boldsymbol b_3\frac{\boldsymbol d\boldsymbol x_2(\boldsymbol t)}{\boldsymbol d\boldsymbol t}

\boldsymbol F_{\boldsymbol a\boldsymbol m\boldsymbol o\boldsymbol r\boldsymbol t\boldsymbol i\boldsymbol g\boldsymbol u\boldsymbol a\boldsymbol d\boldsymbol o\boldsymbol r 4} = \boldsymbol b_4\frac{\boldsymbol d\boldsymbol x_2(\boldsymbol t)}{\boldsymbol d\boldsymbol t}

\boldsymbol F_{\boldsymbol m\boldsymbol a\boldsymbol s\boldsymbol a1} = \boldsymbol m_1\frac{\boldsymbol d^2\boldsymbol x_1(\boldsymbol t)}{\boldsymbol d\boldsymbol t^2}

\boldsymbol F_{\boldsymbol m\boldsymbol a\boldsymbol s\boldsymbol a2} = \boldsymbol m_2\frac{\boldsymbol d^2\boldsymbol x_2(\boldsymbol t)}{\boldsymbol d\boldsymbol t^2}

\boldsymbol F_{\boldsymbol e\boldsymbol x\boldsymbol t\boldsymbol e\boldsymbol r\boldsymbol n\boldsymbol a} = \boldsymbol u(\boldsymbol t)

Paso 2 . Aplicar la segunda Ley de Newton a cada masa por separado de la Figura 14. La primera fila de la derecha es la Ecuación de Equilibrio de fuerzas. Aplicar dicha ecuación por separado a cada masa genera dos ecuaciones de sistema. Las ecuaciones (1) y (2) son La Dinámica del Sistema.

\sum \boldsymbol F_1 = \boldsymbol m_1\frac{\boldsymbol d^2\boldsymbol x_1(\boldsymbol t)}{\boldsymbol d\boldsymbol t^2}

- \boldsymbol k\boldsymbol x_1(\boldsymbol t) - (\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3)\frac{\mathbf d\boldsymbol x_1(\boldsymbol t)}{\mathbf d\boldsymbol t} + \boldsymbol k\boldsymbol x_2\left(\boldsymbol t\right) + \left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3\right)\frac{\boldsymbol d\boldsymbol x_2\left(\boldsymbol t\right)}{\boldsymbol d\boldsymbol t} + \boldsymbol u(\boldsymbol t) = \boldsymbol m_1\frac{\boldsymbol d^2\boldsymbol x_1(\boldsymbol t)}{\boldsymbol d\boldsymbol t^2}\ \ \ (1)

\sum \boldsymbol F _2= \boldsymbol m_2\frac{\boldsymbol d^2\boldsymbol x_2(\boldsymbol t)}{\boldsymbol d\boldsymbol t^2}

\boldsymbol k\boldsymbol x_1(\boldsymbol t) + (\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3)\frac{\mathbf d\boldsymbol x_1(\boldsymbol t)}{\mathbf d\boldsymbol t} - \boldsymbol k\boldsymbol x_2\left(\boldsymbol t\right) - \left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3+ \boldsymbol b_4\right)\frac{\boldsymbol d\boldsymbol x_2\left(\boldsymbol t\right)}{\boldsymbol d\boldsymbol t} = \boldsymbol m_2\frac{\boldsymbol d^2\boldsymbol x_2(\boldsymbol t)}{\boldsymbol d\boldsymbol t^2}\ \ \ (2)

Obtención de X_1(s)/U_(s) y X_2(s)/U_(s).

Paso 3 .Suponiendo todas las condiciones iniciales iguales a cero, se aplican las propiedades de la Transformada de Laplace a cada término de las ecuaciones (1) y (2). Obtenemos las ecuaciones (3) y (4) :

- \boldsymbol k\boldsymbol X_1(\boldsymbol s) - (\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3)\boldsymbol s\boldsymbol X_1\left(\boldsymbol s\right) + \boldsymbol k\boldsymbol X_2\left(\boldsymbol s\right) + \left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3\right)\boldsymbol s\boldsymbol X_2\left(\boldsymbol s\right) + \boldsymbol U(\boldsymbol s) = \boldsymbol m_1\boldsymbol s^2\boldsymbol X_1\left(\boldsymbol s\right);\ \ \ \ \ \ (3)

\boldsymbol k\boldsymbol X_1(\boldsymbol s) + (\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3)\boldsymbol s\boldsymbol X_1\left(\boldsymbol s\right) -\boldsymbol k\boldsymbol X_2\left(\boldsymbol s\right) - \left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3+ \boldsymbol b_4\right)\boldsymbol s\boldsymbol X_2\left(\boldsymbol s\right) = \boldsymbol m_2\boldsymbol s^2\boldsymbol X_2\left(\boldsymbol s\right);\ \ \ \ \ \ (4)

Paso 4 . Se agrupan de manera conveniente los términos de las ecuaciones (3) y (4) y obtenemos las ecuaciones (5) y (6). Cómo se puede intuir, la intención es ordenar para crear un sistema de ecuaciones clásico que permita aplicar álgebra lineal (álgebra de matrices). Se debe tener especial cuidado en el orden del despeje. Observar que la ecuación (5) es el resultado de trasladar los términos del lado izquierdo de la ecuación (3) al lado derecho, excepto la transformada de Laplace de la entrada. Lo mismo debe hacerse entonces con la ecuación (4): sus términos del lado izquierdo se trasladan al lado derecho, y es por eso que en la ecuación (6) aparecen con signos contrarios.

(\boldsymbol m_1\boldsymbol s^2 + \left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3\right)\boldsymbol s + \boldsymbol k)\boldsymbol X_1\left(\boldsymbol s\right) - (\left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3\right)\boldsymbol s + \boldsymbol k)\boldsymbol X_2\left(\boldsymbol s\right) = \boldsymbol U(\boldsymbol s)\ \ \ \ \ \ (5)

- \left(\left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3\right)\boldsymbol s + \boldsymbol k\right)\boldsymbol X_1\left(\boldsymbol s\right) + \left(\boldsymbol m_2\boldsymbol s^2 + \left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3 + \boldsymbol b_4\right)\boldsymbol s + \boldsymbol k\right)\boldsymbol X_2\left(\boldsymbol s\right) = 0\ \ \ \ \ \ (6)

Paso 5 . Para aplicar álgebra lineal, utilizamos las ecuaciones (5) y (6) generadas por la transformada de Laplace para crear el siguiente sistema matricial [A][B]=[C] :

\left[A\right]\left[B\right] = \left[C\right]

\left[\begin{array}{cc} \boldsymbol m_1\boldsymbol s^2 + \left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3\right)\boldsymbol s + \boldsymbol k & - \left(\left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3\right)\boldsymbol s + \boldsymbol k\right) \\ - \left(\left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3\right)\boldsymbol s + \boldsymbol k\right) & \boldsymbol m_2\boldsymbol s^2 + \left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3 + \boldsymbol b_4\right)\boldsymbol s + \boldsymbol k \\ \end{array}\right]\left[\begin{array}{cc} \boldsymbol X_1\left(\boldsymbol s\right) \\ \boldsymbol X_2\left(\boldsymbol s\right) \\ \end{array}\right] = \left[\begin{array}{cc} \boldsymbol U(\boldsymbol s) \\ 0 \\ \end{array}\right]

Paso 6 . Obtenemos el determinante de la matriz A :

\bigtriangleup_{\boldsymbol A}:determinante\ de\ la\ matriz\ A

\bigtriangleup_{\boldsymbol A}=\boldsymbol m_1\boldsymbol m_2\boldsymbol s^4 + \left[\left(\boldsymbol m_1 + \boldsymbol m_2\right)\left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3\right) + \boldsymbol m_1\boldsymbol b_4\right]\boldsymbol s^3 + \left[\left(\boldsymbol m_1 + \boldsymbol m_2\right)\boldsymbol k + \left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3\right)\boldsymbol b_4\right]\boldsymbol s^2 + \boldsymbol b_4\boldsymbol k\boldsymbol s

Cálculo del determinante de la matriz A en Matlab.

Paso 7 . Al aplicar álgebra lineal a la matriz del paso 5, obtenemos X₁(s) y X₂(s) mediante las siguientes fórmulas. Obtenemos las ecuaciones (7) y (8):

X_1(s) = \frac{\left[\begin{array}{cc} \boldsymbol U(\boldsymbol s) & - \left(\left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3\right)\boldsymbol s + \boldsymbol k\right) \\ 0 & \boldsymbol m_2\boldsymbol s^2 + \left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3 + \boldsymbol b_4\right)\boldsymbol s + \boldsymbol k \\ \end{array}\right] }{ \bigtriangleup_{\boldsymbol A}}

X_1(s) = \frac{\boldsymbol U(\boldsymbol s)\left(\boldsymbol m_2\boldsymbol s^2 + \left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3 + \boldsymbol b_4\right)\boldsymbol s + \boldsymbol k \right)}{ \bigtriangleup_{\boldsymbol A}}\ \ \ \ \ \ (7)

\boldsymbol X_2(\boldsymbol s) = \frac{\left[\begin{array}{cc} \boldsymbol m_1\boldsymbol s^2 + \left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3\right)\boldsymbol s + \boldsymbol k & \boldsymbol U(\boldsymbol s) \\ - \left(\left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3\right)\boldsymbol s + \boldsymbol k\right) & 0 \\ \end{array}\right]}{ \bigtriangleup_{\boldsymbol A}}

\boldsymbol X_2(\boldsymbol s) = \frac{\boldsymbol U(\boldsymbol s)\left(\left(\boldsymbol b_1 + \boldsymbol b_2 + \boldsymbol b_3\right)\boldsymbol s + \boldsymbol k\right)}{ \bigtriangleup_{\boldsymbol A}}\ \ \ \ \ \ (8)

De las ecuaciones (7) y (8) se deduce por despeje que las funciones de transferencia H_1(s)=X_1(s)/U_(s) y H_2(s)=X_2(s)/U_(s) del sistema masa-resorte-amortiguador de la Figura 14 son:

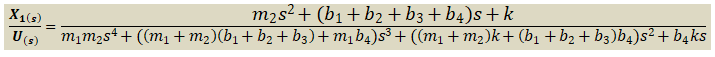
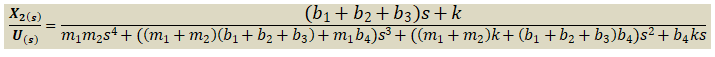
Te puede interesar:

Se resuelven ejercicios de Determinar la Función de Transferencia de sistemas eléctricos, electrónicos, mecánicos, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…

ANEXOS

Cálculo del determinante de la matriz A en Matlab:

>> s=sym('s');
>> k=sym('k');
>> m1=sym('m1');
>> m2=sym('m2');
>> b1=sym('b1');
>> b2=sym('b2');
>> b3=sym('b3');
>> b4=sym('b4');
>> A=[m1*s^2+(b1+b2+b3)*s+k -((b1+b2+b3)*s+k);-((b1+b2+b3)*s+k) m2*s^2+(b1+b2+b3+b4)*s+k]
 
A =
 
[m1*s^2 + (b1 + b2 + b3)*s + k,             - k - s*(b1 + b2 + b3)]
[       - k - s*(b1 + b2 + b3), m2*s^2 + (b1 + b2 + b3 + b4)*s + k]
 
>> delta =det(A)
 
delta =b1*m1*s^3 + b1*m2*s^3 + b2*m1*s^3 + b2*m2*s^3 + b3*m1*s^3 + b3*m2*s^3 + b4*m1*s^3 + k*m1*s^2 + k*m2*s^2 + m1*m2*s^4 + b4*k*s + b1*b4*s^2 + b2*b4*s^2 + b3*b4*s^2

Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos. Al suscribirte podrás contar con excelente material para estudiar y superar con éxito las demandas académicas.

Planes de Suscripción

Curso relacionado:

Sistemas de Control 1

Señales y Sistemas 1