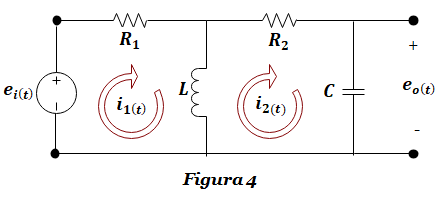
Ejercicio FT-4. Función de Transferencia S. Eléctrico.

Deja un comentario / Análisis de Señales, Análisis de Sistemas Dinámicos, Función de Transferencia, Señales y Sistemas, Sistemas de Control Automático / Por

Ejercicio FT-4: Obtener la función de transferencia G(s)=Eo(s)/Ei(s)  del sistema eléctrico de la Figura 4. La salida es la caída de voltaje e0(t) en los nodos del capacitor, mientras que la entrada es la tensión ei(t) . Aplicar el método de mallas para determinar las ecuaciones diferenciales que representan el modelo del sistema y obtener G(s) a partir de ellas.


figura 4 fteje4

Obtención de la ecuación del sistema. Dinámica del sistema.

Se aplican las técnicas clásicas de análisis de circuitos eléctricos:

Paso 1. Aplicamos la Ley de Voltajes de Kirchhoff al circuito de la Figura 1, considerando que la corriente i1(t) recorre la malla 1, y que la corriente i2(t) recorre la malla 2.

En el diagrama de las mallas 1 y 2 se identifica la caída de voltaje en cada elemento, con su polaridad. Debido a que en el inductor L circulan dos corrientes en diferente dirección, hemos colocado dos caídas de voltaje VL1 (debido a la corriente i1(t)) y VL2 (debido a la corriente i2(t)). Obtenemos las ecuaciones (1) y (2).

figura 1.1 fte4

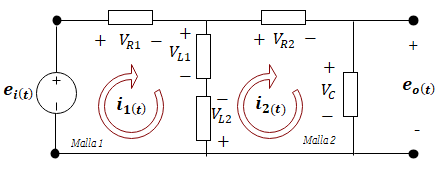
Malla 1:

\boldsymbol V_{\boldsymbol R1} + \boldsymbol V_{\boldsymbol L1} - \boldsymbol V_{\boldsymbol L2} = \boldsymbol e_{\boldsymbol i(\boldsymbol t)};\ \ \ \ \ \ (1)

Malla 2:

- \boldsymbol V_{\boldsymbol L1} + \boldsymbol V_{\boldsymbol R2} + \boldsymbol V_{\boldsymbol L2} + \boldsymbol V_{\boldsymbol C} = 0\ \ \ \ \ \ (2)


Paso 2. Utilizando la relación tensión-corriente en el dominio del tiempo para cada elemento (resistencia, inductor y capacitor), se sustituyen los voltajes de las ecuaciones (1) y (2) por su equivalente. Obtenemos así las ecuaciones (3) y (4), que son en definitiva las ecuaciones del sistema. Debemos tomar en cuenta además que la salida del sistema coincide con el voltaje en el capacitor, es decir e0=VC , ecuación (5):

\boldsymbol V_{\boldsymbol R1} = \boldsymbol R_1\boldsymbol i_{1};\ \ \ \ \ \boldsymbol V_{\boldsymbol R2} = \boldsymbol R_2\boldsymbol i_{2}
\boldsymbol V_{\boldsymbol L1} = \boldsymbol L\frac{\boldsymbol d\boldsymbol i_1}{\boldsymbol d\boldsymbol t};\ \ \ \ \boldsymbol V_{\boldsymbol L2} = \boldsymbol L\frac{\boldsymbol d\boldsymbol i_2}{\boldsymbol d\boldsymbol t}
\boldsymbol V_{\boldsymbol C} = \frac{1}{C}\int\limits_0^ti_2dt
\boldsymbol R_1\boldsymbol i_1 + \boldsymbol L\frac{\boldsymbol d\boldsymbol i_1}{\boldsymbol d\boldsymbol t} - \boldsymbol L\frac{\boldsymbol d\boldsymbol i_2}{\boldsymbol d\boldsymbol t} = \boldsymbol e_{\boldsymbol i}\ ;\ \ \ \ \ \ (3)
 - \boldsymbol L\frac{\boldsymbol d\boldsymbol i_1}{\boldsymbol d\boldsymbol t} + \boldsymbol R_2\boldsymbol i_2 + \boldsymbol L\frac{\boldsymbol d\boldsymbol i_2}{\boldsymbol d\boldsymbol t} + \frac{1}{\boldsymbol C}\int\limits_0^{\boldsymbol t}\boldsymbol i_2\mathbf d\boldsymbol t = 0\ ;\ \ \ \ \ \ (4)
\boldsymbol V_{\boldsymbol C} = \boldsymbol e_0\ ;\ \ \ \ \ \ (5)


Obtención de E0(s)/Ei(s).


Paso 3 . Expresamos en términos generales la Transformada de Laplace (cuyo símbolo es la letra script mayúscula «ℒ») de los término que componen las ecuaciones (3), (4) y (5):

ℒ{f(t)}: transformada de Laplace de la función f(t).

Paso 4 . Suponiendo todas las condiciones iniciales iguales a cero, se aplica la Transformada de Laplace a cada término de las ecuaciones (3), (4) y (5). Obtenemos las ecuaciones (6), (7) y (8):

En General:

\mathbf{\mathcal{L}}\left\{\boldsymbol R\boldsymbol i_{(\boldsymbol t)}\right\} = \boldsymbol R\boldsymbol I_{(\boldsymbol s)};\ \ \ \ \ \ \mathbf{\mathcal{L}}\left\{\boldsymbol L\frac{\boldsymbol d\boldsymbol i_{(\boldsymbol t)}}{\boldsymbol d\boldsymbol t}\right\} = \boldsymbol L\boldsymbol s\boldsymbol I_{(\boldsymbol s)}
\mathbf{\mathcal{L}}\left\{\frac{1}{\boldsymbol C}\int\limits_0^{\boldsymbol t}\boldsymbol i_{(\boldsymbol t)}\mathbf d\boldsymbol t\right\} = \frac{1}{\boldsymbol C\boldsymbol s}\boldsymbol I_{(\boldsymbol s)}
\boldsymbol R_1\boldsymbol I_{1(\boldsymbol s)} + \boldsymbol L\boldsymbol s\boldsymbol I_{1\left(\boldsymbol s\right)} - \boldsymbol L\boldsymbol s\boldsymbol I_{2\left(\boldsymbol s\right)} = \boldsymbol E_{\boldsymbol i(\boldsymbol s)};\ \ \ \ \ \ (6)
 - \boldsymbol L\boldsymbol s\boldsymbol I_{1\left(\boldsymbol s\right)} + \boldsymbol R_2\boldsymbol I_{2\left(\boldsymbol s\right)} + \boldsymbol L\boldsymbol s\boldsymbol I_{2\left(\boldsymbol s\right)} + \frac{1}{\boldsymbol C\boldsymbol s}\boldsymbol I_{2\left(\boldsymbol s\right)} = 0;\ \ \ \ \ \ (7)
\frac{1}{\boldsymbol C\boldsymbol s}\boldsymbol I_{2\left(\boldsymbol s\right)} = \boldsymbol E_{0\left(\boldsymbol s\right)};\ \ \ \ \ \ (8)


Paso 5. Con el fin de crear un sistema de matrices, se agrupan de manera conveniente los términos de las ecuaciones (6) y (7), obtenemos las ecuaciones (9) y (10):

(\boldsymbol L\boldsymbol s + \boldsymbol R_1)\boldsymbol I_{1\left(\boldsymbol s\right)} - \boldsymbol L\boldsymbol s\boldsymbol I_{2\left(\boldsymbol s\right)} = \boldsymbol E_{\boldsymbol i(\boldsymbol s)};\ \ \ \ \ \ (9)
 - \boldsymbol L\boldsymbol C\boldsymbol s^2\boldsymbol I_{1\left(\boldsymbol s\right)} + (\boldsymbol L\boldsymbol C\boldsymbol s^2 + \boldsymbol C\boldsymbol R_2\boldsymbol s + 1)\boldsymbol I_{2\left(\boldsymbol s\right)} = 0;\ \ \ \ \ \ (10)

Paso 6 . Utilizamos las ecuaciones (9) y (10) para crear el siguiente sistema matricial:

\left[A\right]\left[B\right] = \left[C\right]
\left[\begin{array}{cc} \boldsymbol L\boldsymbol s + \boldsymbol R_1 &  - \boldsymbol L\boldsymbol s \\  - \boldsymbol L\boldsymbol C\boldsymbol s^2 & \boldsymbol L\boldsymbol C\boldsymbol s^2 + \boldsymbol C\boldsymbol R_2\boldsymbol s + 1 \\  \end{array}\right]\left(\begin{array}{cc} \boldsymbol I_{1\left(\boldsymbol s\right)} \\ \boldsymbol I_{2\left(\boldsymbol s\right)} \\  \end{array}\right) = \left(\begin{array}{cc} \boldsymbol E_{\mathbf i\left(\boldsymbol s\right)} \\ 0 \\  \end{array}\right)


Paso 7. Obtenemos el determinante de la matriz A:

 \bigtriangleup_{\boldsymbol A}:determinante\ de\ la\ matriz\ A
 \bigtriangleup_{\boldsymbol A}=\boldsymbol L\boldsymbol C\left(\boldsymbol R_1 + \boldsymbol R_2\right)\boldsymbol s^2 + \left(\mathbf L + \boldsymbol C\boldsymbol R_1\boldsymbol R_2\right)\boldsymbol s + \boldsymbol R_1

Cálculo del determinante de la matriz A en Matlab.



Paso 8 . Al aplicar álgebra lineal a la matriz del paso 6, obtenemos I2(s) mediante la siguiente fórmula. Obtenemos la ecuación (11):

I_2(s) = \frac{\left[\begin{array}{cc} \boldsymbol L\boldsymbol s + \boldsymbol R_1 & \boldsymbol E_{\boldsymbol i(\boldsymbol s)} \\  - \boldsymbol L\boldsymbol C\boldsymbol s^2 & 0 \\  \end{array}\right]}{ \bigtriangleup_{\boldsymbol A}}
I_2(s) = \frac{\boldsymbol E_{\boldsymbol i(\boldsymbol s)}(\boldsymbol L\boldsymbol C\boldsymbol s^2)}{ \bigtriangleup_{\boldsymbol A}}
\boldsymbol I_{2(\boldsymbol s)} = \frac{\boldsymbol E_{\boldsymbol i(\boldsymbol s)}(\boldsymbol L\boldsymbol C\boldsymbol s^2)}{\boldsymbol L\boldsymbol C\left(\boldsymbol R_1 + \boldsymbol R_2\right)\boldsymbol s^2 + \left(\mathbf L + \boldsymbol C\boldsymbol R_1\boldsymbol R_2\right)\boldsymbol s + \boldsymbol R_1};\ \ \ \ \ \ (11)


Paso 9. Utilizamos la ecuación (8), despejamos I2(s), sustituimos allí el resultado obtenido para I2(s) en la ecuación (11), y obtenemos la igualdad de la ecuación (12):

 \boldsymbol I_{2(\boldsymbol s)} = \boldsymbol C\boldsymbol s\boldsymbol E_{0(\boldsymbol s)}
\frac{\boldsymbol E_{\boldsymbol i(\boldsymbol s)}(\boldsymbol L\boldsymbol C\boldsymbol s^2)}{\boldsymbol L\boldsymbol C\left(\boldsymbol R_1 + \boldsymbol R_2\right)\boldsymbol s^2 + \left(\mathbf L + \boldsymbol C\boldsymbol R_1\boldsymbol R_2\right)\boldsymbol s + \boldsymbol R_1} = \boldsymbol C\boldsymbol s\boldsymbol E_{0(\boldsymbol s)};\ \ \ \ \ \ (12)

De la ecuación (12) se deduce por despeje que la función de transferencia G(s)=Eo(s)/Ei(s)  de la Figura 4 es:


figura 4.2 ft4

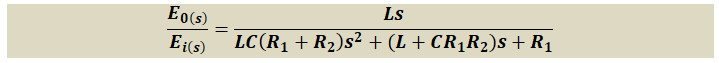
Te puede interesar:

  • Se resuelven ejercicios de Determinar la Función de Transferencia de sistemas eléctricos, electrónicos, mecánicos, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
  • Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
  • Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
  • Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
  • Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…

ANEXOS

Cálculo del determinante de la matriz A en Matlab:
>> s=sym('s');
>> R1=sym('R1');
>> R2=sym('R2');
>> C=sym('C');
>> L=sym('L');
>> A=[L*s+R1 -L*s;-L*C*s^2 L*C*s^2+C*R2*s+1]
 
A =
 
[R1 + L*s,                 -L*s]
[-C*L*s^2, C*L*s^2 + C*R2*s + 1]
 
 
>> delta=det(A)
 
delta = R1 + L*s + C*L*R1*s^2 + C*L*R2*s^2 + C*R1*R2*s

                     %este es un comentario... Por lo tanto:
                          ∆ = (R1+R2)*C*L*s^2 + (L+C*R1*R2)*s + R1

Artículos relacionados:

Función de Transferencia – Teoría

Diagrama de Bloques – Teoría y Práctica.

Función de Transferencia – S. Mecánico – Ejercicio resuelto 3

Función de Transferencia – S. Mecánico – Ejercicio resuelto 2

Prof. Larry. Estudios:

Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.

Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs

Related Posts

error: Content is protected !!
Scroll al inicio