Función de Transferencia S. MRA – Ejercicio resuelto 1. -

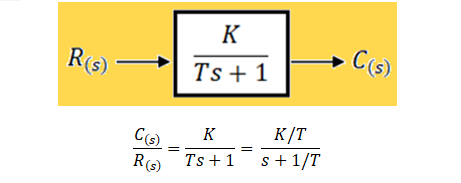
Ejercicio FT-1: Obtener la función de transferencia H_(s)=X_(s)/U_(s) del sistema masa-resorte-amortiguador de la Figura 1. La salida es el desplazamiento x_(t) del sistema, mientras que la entrada es la fuerza u_(t) que se ejerce sobre la masa m.

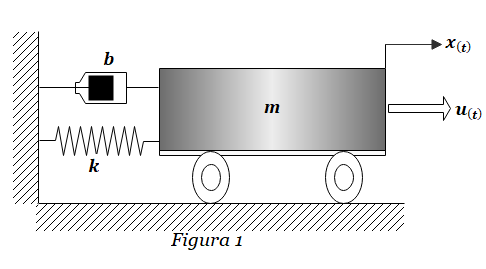
Obtención de la ecuación del sistema. Dinámica del sistema.

Las fuerzas que intervienen en el movimiento (o dinámica) del sistema son las siguientes:

Paso 1. En un sistema masa-resorte-amortiguador, el resorte representa toda fuerza capaz de producir un movimiento oscilatorio armónico. Llamamos a esta fuerza F_resorte y se calcula mediante la Ley de Hooke. Por inercia, la masa m se opone a cambiar su estado de movimiento mediante una F_masa.

Las unidades utilizadas son: x:desplazamiento (m) ; t: tiempo (s); k:constante de elasticidad (N/m); m: unidad de masa. (N-s²/m)

Mientras, la constante de fricción viscosa del amortiguador representa toda fuerza de fricción en general, como por ejemplo, el roce con una superficie determinada. Llamamos a esta fuerza F_amortiguador. Consideramos además que las ruedas experimentan fuerza de roce igual a cero cuando se desplazan sobre la superficie. La otra fuerza que influye en el movimiento es la fuerza externa F_externa ejercida directamente sobre la masa, denominada u(t) en el esquema mecánico.

b:constante de fricción viscosa. (N-s/m); u(t): Fuerza (N)

\boldsymbol F_{\boldsymbol r\boldsymbol e\boldsymbol s\boldsymbol o\boldsymbol r\boldsymbol t\boldsymbol e} = \boldsymbol k\boldsymbol x(\boldsymbol t)

\boldsymbol F_{\boldsymbol a\boldsymbol m\boldsymbol o\boldsymbol r\boldsymbol t\boldsymbol i\boldsymbol g\boldsymbol u\boldsymbol a\boldsymbol d\boldsymbol o\boldsymbol r} = \boldsymbol b\frac{\boldsymbol d\boldsymbol x(\boldsymbol t)}{\boldsymbol d\boldsymbol t}

\boldsymbol F_{\boldsymbol m\boldsymbol a\boldsymbol s\boldsymbol a} = \boldsymbol m\frac{\boldsymbol d^2\boldsymbol x(\boldsymbol t)}{\boldsymbol d\boldsymbol t^2}

\boldsymbol F_{\boldsymbol e\boldsymbol x\boldsymbol t\boldsymbol e\boldsymbol r\boldsymbol n\boldsymbol a} = \boldsymbol u(\boldsymbol t)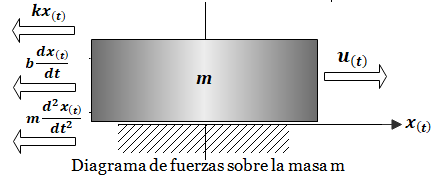

Paso 2. Aplicamos la segunda Ley de Newton de la siguiente manera: Las fuerzas que participan en el movimiento se suman a la izquierda de la ecuación (1). De ellas, las fuerzas que se oponen al movimiento tendrán signo negativo (restan) y las que impulsan el movimiento tendrán signo positivo (suman):

\sum \boldsymbol F = \boldsymbol m\frac{\boldsymbol d^2\boldsymbol x(\boldsymbol t)}{\boldsymbol d\boldsymbol t^2}

- \boldsymbol k\boldsymbol x\left(\boldsymbol t\right) - \boldsymbol b\frac{\boldsymbol d\boldsymbol x\left(\boldsymbol t\right)}{\boldsymbol d\boldsymbol t} + \boldsymbol u(\boldsymbol t) = \boldsymbol m\frac{\boldsymbol d^2\boldsymbol x(\boldsymbol t)}{\boldsymbol d\boldsymbol t^2}\boldsymbol ;\ \ \ \ \ \ (1)

Obtención de X_(s)/U_(s).

Paso 3 . Suponiendo todas las condiciones iniciales iguales a cero, se aplican las propiedades de la Transformada de Laplace (cuyo símbolo es la letra script mayúscula «ℒ») a cada término de la ecuación (1). Obtenemos la ecuación (2):

ℒ{f(t)}: transformada de Laplace de la función f(t).

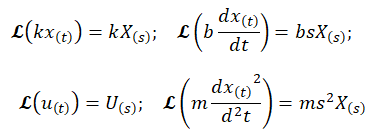
- \boldsymbol k\boldsymbol X(\boldsymbol s) - \boldsymbol b\boldsymbol s\boldsymbol X\left(\boldsymbol s\right) + \boldsymbol U(\boldsymbol s) = \boldsymbol m\boldsymbol s^2\boldsymbol X\left(\boldsymbol s\right)\ \ \ \ \ \ (2)

Paso 4. Se agrupan de manera conveniente los términos de la ecuación (2) y obtenemos la ecuación (3):

U(s) = ms^2X\left(s\right) + kX\left(s\right) + bsX\left(s\right)

\left\{\boldsymbol m\boldsymbol s^2 + \boldsymbol b\boldsymbol s + \boldsymbol k\right\}\boldsymbol X\left(\boldsymbol s\right) = \boldsymbol U\left(\boldsymbol s\right)\ \ \ \ \ \ (3)

De la ecuación (3) se deduce por despeje que la función de transferencia H_(s)=X_(s)/U_(s) de la Figura 1 es:

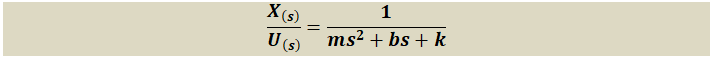
Te puede interesar:

Se resuelven ejercicios de Determinar la Función de Transferencia de sistemas eléctricos, electrónicos, mecánicos, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…

Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos. Al suscribirte podrás contar con excelente material para estudiar y superar con éxito las demandas académicas.

Planes de Suscripción

Curso relacionado:

Sistemas de Control 1

Señales y Sistemas 1