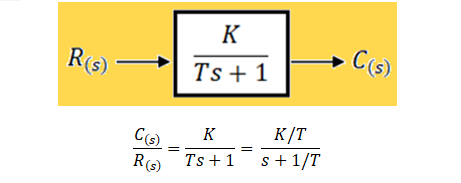
La Función de Transferencia H(s) es el cociente formado por Y(s), la Transformada de Laplace de la salida de un Sistema LIT (Causal, Lineal e Invariante en el tiempo), dividida entre X(s), la Transformada de Laplace de la entrada a dicho sistema, cuando las condiciones iniciales son iguales a cero. Como se muestra en la Figura 1, la Función de Transferencia permite representar un sistema mediante una herramienta gráfica que muestra el flujo de información a través de todos los componentes del mismo: El diagrama de bloques.
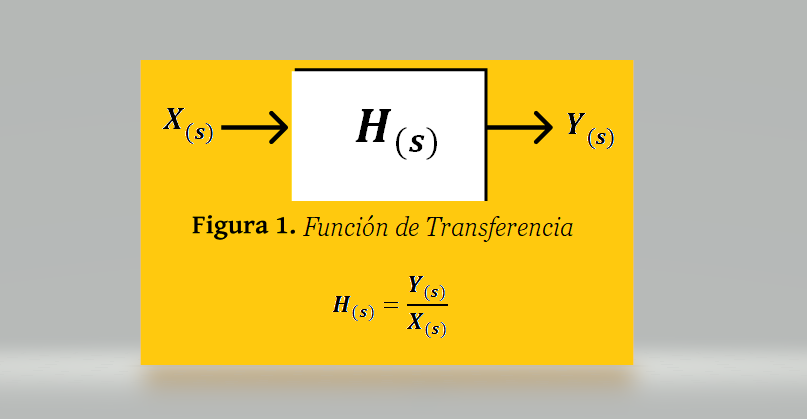
Concepto de Función de Transferencia
La Función de Transferencia H(s) de un sistema LIT analógico se define como la Transformada de Laplace de la Respuesta al Impulso, o respuesta impulsional h(t), de dicho sistema. Entonces:
\boldsymbol H(\boldsymbol s) = \mathbf{\mathcal{L}}\left\{\boldsymbol h_{(\boldsymbol t)}\right\} = \int\limits_{- \mathbf \infty}^{\mathbf \infty}\boldsymbol h(\boldsymbol t)\boldsymbol e^{- \boldsymbol s\boldsymbol t}\mathbf d\boldsymbol t;\ \ \ \ \ \ \ (1)Dónde:
\mathbf{\mathcal{L}}:símbolo\ de\ la\ Transformada\ de\ Laplace\mathbf{\mathcal{L}}\left\{\boldsymbol h_{(\boldsymbol t)}\right\}:Transformada\ de\ Laplace\ de\ la\ función\ h(t)Supongamos que tenemos un sistema LIT llamado S. Debido a que el Sistema S está totalmente caracterizado por su respuesta impulsional h(t), entonces la función de transferencia H(s) del Sistema S, definida por la ecuación (1), también caracteriza entera y completamente al Sistema S.
Sean x(t) la señal de entrada al sistema S, y y(t) la señal de salida del sistema S, tal como se observa en la Figura 2:
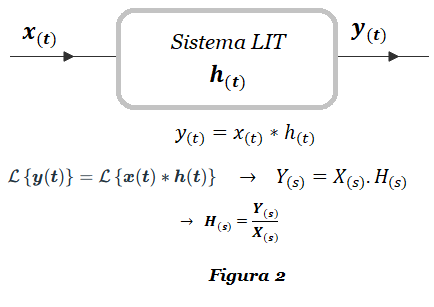
Las tres señales x(t), y(t) y h(t) se relacionan entre sí mediante la operación de convolución:
\boldsymbol y(\boldsymbol t) = \boldsymbol x(\boldsymbol t)*\boldsymbol h(\boldsymbol t);\ \ \ \ \ \ (2)
Aplicaremos la Transformada de Laplace a ambos lados de la ecuación (2):
\mathbf{\mathcal{L}}\left\{\boldsymbol y(\boldsymbol t)\right\} = \mathbf{\mathcal{L}}\left\{\boldsymbol x(\boldsymbol t)*\boldsymbol h(\boldsymbol t)\right\}Y obtenemos la ecuación (3):
\boldsymbol Y(\boldsymbol s) = \boldsymbol X(\boldsymbol s)H(\boldsymbol s);\ \ \ \ \ \ (3)
Al igual que la ecuación (1), la ecuación (3) nos permite obtener la Función de Transferencia del Sistema S :
\boldsymbol H(\boldsymbol s) = \frac{Y(\boldsymbol s)}{X(\boldsymbol s)};\ \ \ \ \ \ (4)La ecuación (4) tiene una consecuencia muy importante para la ingeniería en general, y es que conociendo la relación entrada-salida de un sistema LIT, tenemos todo lo necesario para determinar la respuesta impulsiva de dicho sistema de una manera algebraica (evitando el cálculo de integrales), lo cual representa una de las grandes ventajas de utilizar la Transformada de Laplace.
Alternativamente, si conocemos la Función de Transferencia de un sistema, seremos capaces de determinar la salida y(t) de dicho sistema en el dominio del tiempo para cualquier señal de entrada x(t) del mismo. Aplicando antitransformada de Laplace a la ecuación (3) obtenemos la ecuación de la salida en el tiempo, y(t):
\boldsymbol y(\boldsymbol t) = \mathbf{\mathcal{L}}^{- 1}(\boldsymbol Y(\boldsymbol s))Y aplicando antitransformada de Laplace a la ecuación (4) obtenemos la respuesta impulsiva, h(t):
\boldsymbol h(\boldsymbol t) = \mathbf{\mathcal{L}}^{- 1}(\boldsymbol H(\boldsymbol s))Existe una manera de estudiar la respuesta del sistema sin necesidad de aplicar antitransformada, y es mediante el estudio de los polos y ceros del sistema.
Polos y ceros de la Función de Transferencia
Los polos y ceros de la Función de Transferencia permiten estudiar la respuesta del sistema a entradas típicas de prueba (impulso, escalón, rampa) sin tener que realizar la transformada inversa de Laplace. La Función de Transferencia G(s) estándar tiene la siguiente forma:
G(s) = \frac{Y(s)}{X(s)} = \frac{b_ms^m + b_{m - 1}s^{m - 1} + \ldotp \ldotp \ldotp + b_1s + b_0}{s^n + a_{n - 1}s^{n - 1} + \ldotp \ldotp \ldotp + a_1s + a_0}Se conoce como Polinomio Característico p(s) de la Función de Transferencia al denominador de G(s).
Polinomio\ Característico:\ \ \ \boldsymbol p(\boldsymbol s) = \boldsymbol s^{\boldsymbol n} + \boldsymbol a_{\boldsymbol n - 1}\boldsymbol s^{\boldsymbol n - 1} + \ldotp \ldotp \ldotp + \boldsymbol a_1\boldsymbol s + \boldsymbol a_0El Orden del Sistema es el grado del Polinomio Característico, es decir, el valor de n. A continuación se define lo que son Los Polos y Los Ceros del sistema:
- Polos del Sistema: valores dela variable «s» que hacen que G(s) tienda a infinito. Son las raíces del Polinomio Característico.
- Ceros del Sistema: valores dela variable «s» que hacen que G(s) sea igual a cero. Son las raíces del Numerador de G(s).
\boldsymbol P\boldsymbol o\boldsymbol l\boldsymbol o\boldsymbol s\ del\ Sistema:valores\ de\ "s"\ tal\ que\ \boldsymbol G(\boldsymbol s)\rightarrow \mathbf \infty
\boldsymbol C\boldsymbol e\boldsymbol r\boldsymbol o\boldsymbol s\ del\ Sistema:\ valores\ de\ "s"\ tal\ que\ \boldsymbol G(\boldsymbol s) = 0
Más adelante veremos que al graficar el Lugar Geométrico de las Raíces, la cantidad de Ceros debe igualar a la cantidad de Polos. Por lo tanto, algunos Ceros pueden estar en el infinito, ya que cuando el valor de la variable «s» tiende a infinito, el polinomio característico (es decir, el denominador) tiende a infinito y por definición G(s) tiende a Cero.
La ubicación de los Polos en el Plano «s» tiene especial interés a la hora de analizar la estabilidad absoluta del sistema:
Un sistema es estable si todos sus polos están situados en el semiplano complejo negativo (semiplano izquierdo);
Un sistema es inestable si alguno de sus polos está situado en el semiplano complejo positivo (semiplano derecho);
Un sistema es marginalmente estable si sus polos están situados en el semiplano complejo negativo, excepto uno o más situados en el eje imaginario.
Relación entrada-salida del sistema.
La relación entrada-salida de un sistema es aquella expresión algebraica, por lo general una Ecuación Diferencial del Sistema (EDS), que nos permite conocer la señal de salida y(t) en función de la señal de entrada x(t).
Por ejemplo, un sistema de primer orden es aquel cuya relación entrada-salida en el dominio del tiempo, está definida por una ecuación diferencial de primer orden del tipo:
\frac{\boldsymbol d\boldsymbol y(\boldsymbol t)}{\boldsymbol d\boldsymbol t} + \boldsymbol a_0\boldsymbol y(\boldsymbol t) = \frac{\boldsymbol d\boldsymbol x\left(\boldsymbol t\right)}{\boldsymbol d\boldsymbol t} + \boldsymbol b_0\boldsymbol x\left(\boldsymbol t\right);\ para\ cada\ t\text{∈}\text{R}La Ecuación Diferencial del Sistema (EDS) es un modelo dinámico que establece una restricción fundamental sobre ciertas combinaciones de la entrada, la salida y algunas derivadas de ambas señales.
La relación entrada-salida de un sistema puede ser una simple expresión algebraica que nos permita directamente determinar la salida en función de la entrada. Sea la siguiente relación entrada-salida del sistema S1:
\boldsymbol y(\boldsymbol t) = \boldsymbol t\boldsymbol x(\boldsymbol t)
Dada una señal x(t) cualquiera, utilizando la ecuación anterior podemos conocer la expresión de salida y(t) del sistema S1.
Si la entrada x(t) al sistema S1 es la siguiente:
x\left(t\right) = u(t - 1) - u(t - 3)
Entonces la salida y(t) del sistema S1 es:
y(t) = tx(t)\ \ \rightarrow\ \ \boldsymbol y\left(\boldsymbol t\right) = \boldsymbol t(\boldsymbol u(\boldsymbol t - 1) - \boldsymbol u(\boldsymbol t - 3))
En este contexto, la Función de Transferencia de un sistema LIT analógico viene a ser el elemento que conecta la relación entrada-salida de dicho sistema con su respuesta impulsional h(t). Es decir, podemos obtener una a partir de la otra mediante el siguiente proceso:
- Si queremos obtener h(t) para un sistema en particular del cual sólo poseemos un esquema gráfico, debemos obtener en primer lugar la relación entrada-salida del sistema utilizando leyes de la física (ver ejemplos en el siguiente apartado), luego aplicar la transforma de Laplace a la EDS obtenida, despejar la función de transferencia H(s) y finalmente aplicar la antitransformada de Laplace, lo que nos proporciona la expresión matemática para h(t).
- Si por el contrario, queremos obtener la EDS del sistema a partir de su respuesta impulsional h(t), aplicaremos la transforma de Laplace a la ecuación de h(t), es decir, obtenemos la Función de Transferencia H(s), y con ésta última podemos obtener la EDS del sistema aplicando las propiedades de la Transformada de Laplace.
Función de Transferencia a Lazo abierto – cerrado. FT Directa.
Para entender los conceptos de Función de Transferencia a lazo abierto, o Función de Transferencia a lazo cerrado y Función de Transferencia visita FT a lazo abierto y FT a lazo cerrado.
Ejercicios resueltos de Función de Transferencia
El objetivo en los siguientes ejercicios es determinar la relación entrada-salida del sistema utilizando leyes de la física, para luego aplicar la transforma de Laplace a la EDS obtenida y despejar de este resultado la función de transferencia H(s) .
Ejercicio FT-1: Obtener la función de transferencia H(s)=X(s)/U(s) del sistema masa-resorte-amortiguador de la Figura 1. La salida es el desplazamiento x(t) del sistema, mientras que la entrada es la fuerza u(t) que se ejerce sobre la masa m.
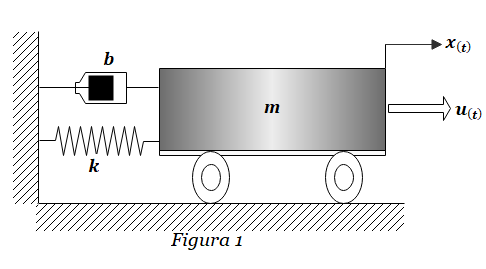
Encontrarás la solución al ejercicio FT-1 en el siguiente link: SOLUCIÓN Ejercicio FT-1.
Ejercicio FT-2: Obtener la función de transferencia H1(s)=X1(s)/U(s) y H2(s)=X2(s)/U(s) del sistema masa-resorte-amortiguador de la Figura 2.
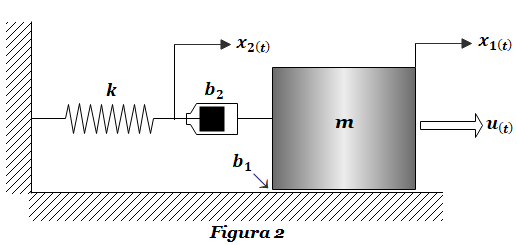
Encontrarás la solución al ejercicio FT-2 en el siguiente link: SOLUCIÓN Ejercicio FT-2.
Ejercicio FT-3: Obtener la función de transferencia H1(s)=X1(s)/U(s) y H2(s)=X2(s)/U(s) del sistema masa-resorte-amortiguador de la Figura 3. Ilustrar el uso de diagramas de cuerpo libre..
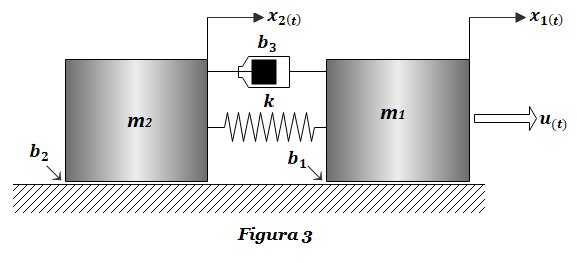
Encontrarás la solución al ejercicio FT-3 en el siguiente link: SOLUCIÓN Ejercicio FT-3.
Ejercicio FT-4: Obtener la función de transferencia G(s)=Eo(s)/Ei(s) del sistema eléctrico de la Figura 4. La salida es la caída de voltaje e0(t) en los nodos del capacitor, mientras que la entrada es la tensión ei(t) . Aplicar el método de mallas para determinar las ecuaciones diferenciales que representan el modelo del sistema y obtener G(s) a partir de ellas.
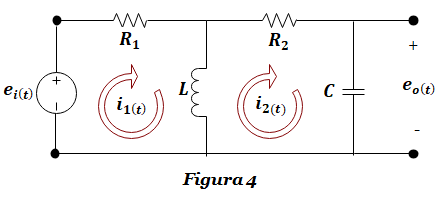
Encontrarás la solución al ejercicio FT-4 en el siguiente link: SOLUCIÓN Ejercicio FT-4.
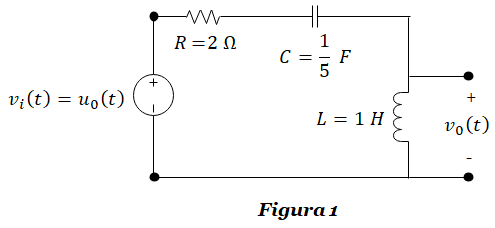
PROBLEMA 1.1: Calcula la expresión de la salida v0(t) en función del tiempo para el circuito RLC de la Figura 1, ante una entrada vi(t)=u0(t) (escalón unitario) con R=2 Ω, L=1 H y C=1/5 F. Considere las condiciones iniciales iguales a cero.
Encontrarás la solución al Problema 1-1 en el siguiente link: SOLUCIÓN Examen 1-1.
Te puede interesar:
- Se resuelven ejercicios de Señales y Sistemas, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry Obando, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…
Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos. Al suscribirte podrás contar con excelente material para estudiar y superar con éxito las demandas académicas.
Curso relacionado:
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs