La Transformada de Laplace es una herramienta matemática de gran importancia ya que permite analizar las características de señales y sistemas LIT analógicos en el Dominio Transformado de Laplace que se ilustra en La Figura. Es decir, fuera del dominio del tiempo, lo que ofrece al ingeniero la ventaja de cambiar operaciones complejas con derivadas e integrales, por operaciones aritméticas habituales del álgebra, como la suma y el producto.

Transformada de Laplace – Definición
Para una señal cualquiera x(t) , la siguiente notación se debe interpretar como «X(s) es La Transformada de Laplace de la función x(t) « :
\boldsymbol X(\boldsymbol s) = \mathbf{\mathcal{L}}\left(\boldsymbol x(\boldsymbol t)\right)Una notación equivalente sería:
\boldsymbol x(\boldsymbol t)\mathop{\leftrightarrow}\limits^{\mathbf{\mathcal{L}}}\boldsymbol X(\boldsymbol s),\ \ \ \ \boldsymbol R\boldsymbol O\boldsymbol CDonde ROC significa Región de Convergencia y es la región del Dominio Transformado donde se localizan los valores de la variable «s» para los cuáles X(s) está definida.
La ecuación (1), llamada ecuación de análisis, permite obtener directamente la Transformada de Laplace X(s) a partir de la función x(t) :
\boldsymbol X(\boldsymbol s) = \int\limits_{- \mathbf \infty}^{\mathbf \infty}\boldsymbol x(\boldsymbol t)\boldsymbol e^{- \boldsymbol s\boldsymbol t}\mathbf d\boldsymbol t\ \ \ \ \ (1)En la ecuación (1), la variable «s» es una variable compleja definida generalmente como:
s = \alpha + j\omega
Es decir, que la ecuación (1) podría escribirse como:
\boldsymbol X(\alpha + j\omega ) = \int\limits_{- \mathbf \infty}^{\mathbf \infty}\boldsymbol x(\boldsymbol t)\boldsymbol e^{- \boldsymbol \alpha \boldsymbol t}\boldsymbol e^{- \mathbf j\mathbf \omega \boldsymbol t}\mathbf d\boldsymbol t\ \ \ \ \ (2)En la ecuación (2), si la parte real de la variable «s» es igual a cero, es decir, si α =0, entonces la ecuación (2) se convierte en La Transformada de Fourier :
\alpha = 0,\Rightarrow TransformadadeFourier:\boldsymbol X(j\omega ) = \int\limits_{- \mathbf \infty}^{\mathbf \infty}\boldsymbol x(\boldsymbol t)\boldsymbol e^{- \mathbf j\mathbf \omega \boldsymbol t}\mathbf d\boldsymbol t\ \ \ \ \ (3)Volviendo a la ecuación (1), la señal X(s) es una señal compleja de variable compleja. Más que estar interesados en representar gráficamente la señal X(s), la ingeniería estará más enfocada en la localización de Los Polos y Ceros de X(s) .
Diagrama de Polos Y Ceros de La Transformada de Laplace
El Diagrama de Polos y Ceros de X(s) es una representación gráfica sobre el Plano Complejo «s» de los polos y ceros de la señal X(s) . La Figura 1 ilustra que El Plano Complejo «s» (también llamado por algunas escuelas Dominio Transformado de Laplace) es simplemente un sistema cartesiano que identifica a la variable real α con el eje de las abscisas, mientras que la variable imaginaria ω está representada con el eje de las ordenadas:
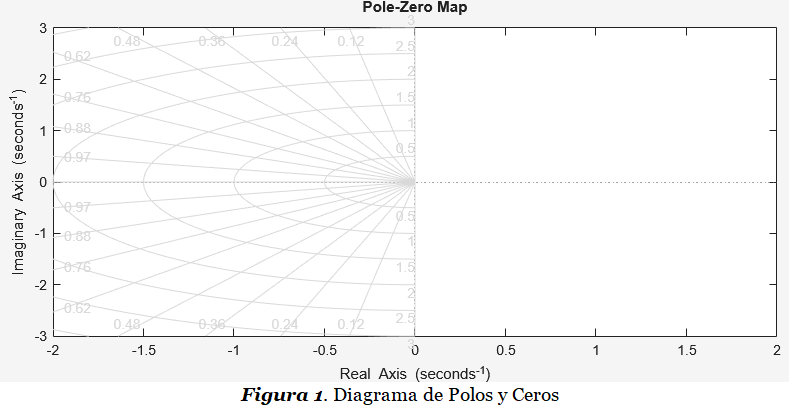
Observar en la Figura 1 que la unidad de la variable «s» es «segundos-1«. Es así porque, por defecto, cuando se obtiene la Transformada de Laplace con la ecuación (1), la variable eliminada es el tiempo, cuya unidad es el segundo.
- La ubicación de un cero en el plano «s» se simboliza con un círculo (○).
- La coincidencia de dos o más ceros en la misma coordenada, se simboliza añadiendo un superíndice al círculo (○2 , ○3, …)
- La ubicación de un polo en el plano «s» se simboliza con una cruz (×).
- La coincidencia de dos o más polos en la misma coordenada, se simboliza añadiendo un superíndice a la cruz (×2 , ×3, …)
La principal ventaja de utilizar La Transformada de Laplace es que permite transformar ecuaciones diferenciales en fracciones de polinomios.
Por lo general, en el ámbito del Análisis de Señales y Sistemas, la señal X(s) tendrá la forma de un cociente de polinomios:
X(s) = \frac{B(s)}{A(s)} = \frac{b_ms^m + b_{m - 1}s^{m - 1} + \ldotp \ldotp \ldotp + b_1s + b_0}{a_ns^n + a_{n - 1}s^{n - 1} + \ldotp \ldotp \ldotp + a_1s + a_0}Como ejemplo en la Figura 2 se observa la ubicación de los polos y ceros del Sistema S1, cuya Función de Transferencia X(s) se muestra a continuación:
X(s) = \frac{s + 0.5}{s^2 + 2s + 22}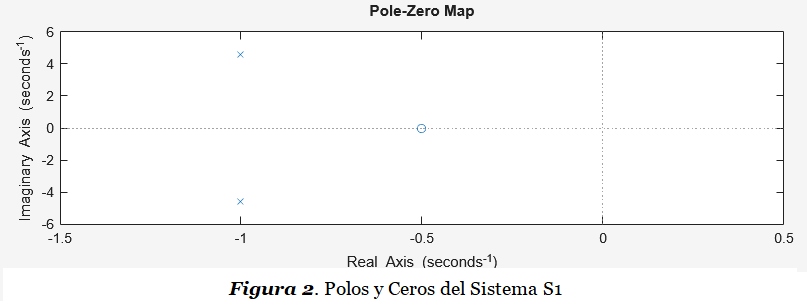
La Función de Transferencia es el cociente formado por La Transformada de Laplace (TL) de la salida entre la TL de la entrada. La Función de Transferencia es a su vez la TL de la respuesta impulsiva.
En el ejemplo anterior, si X(s) es la Función de Transferencia del sistema S1, entonces se sobrentiende que el polinomio B(s) es la TL de la salida, mientras que el polinomio A(s) es la TL de la entrada. Para consultar la teoría sobre Función de Transferencia visita Función de Transferencia.
En el ejemplo anterior vemos que calcular matemáticamente lo polos y ceros de una función X(s) cualquiera implica factorizar los polinomios A(s) y B(s). Utilizamos nuevamente el sistema S1 como ejemplo. Veremos en la Figura 3 que la simulación confirma los resultados obtenidos al factorizar:
X(s) = \frac{B(s)}{A(s)}= \frac{s + 0.5}{s^2 + 2s + 22}= \frac{s + 0.5}{(s+1-j4.5826)(s+1+j4.5826)}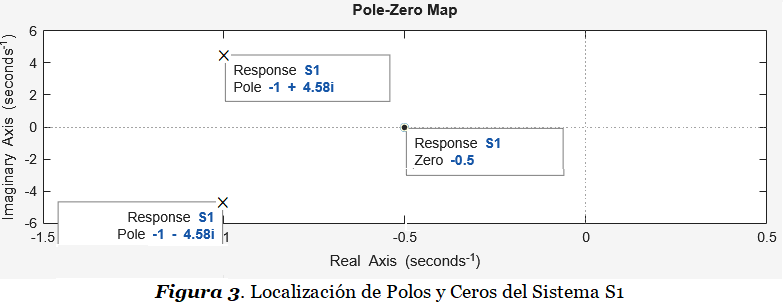
Tabla de Transformadas Típicas de Laplace
Por lo general, no se requiere obtener la Transformada de Laplace mediante la ecuación (1). El ingeniero debe aprovechar el camino recorrido al representar señales y sistemas con funciones básicas. Para un repaso ver Señales Elementales.
En la Tabla 1 podemos ver la Transformada de Laplace de las funciones típicas utilizadas en el Análisis de señales y sistemas LIT analógicos. En la notación utilizada en la Tabla 1 se cumple que a , ω0 son constantes reales, mientras que n es un número entero mayor o igual a 1:
\boldsymbol x(\boldsymbol t)\mathop{\leftrightarrow}\limits^{\mathbf{\mathcal{L}}}\boldsymbol X(\boldsymbol s),\boldsymbol R\boldsymbol O\boldsymbol C\boldsymbol a,\omega_0,n\ \ \ son\ constantes
\boldsymbol a,\omega_0 \in {\mathbb{R}}; \ \ \ \omega_0 > 0n \in {\mathbb{Z}};\ \ \ n \geq 1| x(t) | X(s) | ROC |
| δ(t) | 1 | ∀s |
| u(t) | 1/s | ℝe(s)>0 |
| -u(-t) | 1/s | ℝe(s)<0 |
| tu(t) | 1/s2 | ℝe(s)>0 |
| [(tn-1)/((n-1)!)]u(t) | 1/sn | ℝe(s)>0 |
| -[(tn-1)/((n-1)!)]u(-t) | 1/sn | ℝe(s)<0 |
| e-atu(t) | 1/(s+a) | ℝe(s) > -a |
| -e-atu(-t) | 1/(s+a) | ℝe(s) < -a |
| te-atu(t) | 1/(s+a)2 | ℝe(s) > -a |
| -te-atu(-t) | 1/(s+a)2 | ℝe(s) < -a |
| (tn-1)/((n-1)!)e-atu(t) | 1/(s+a)n | ℝe(s) > -a |
| cos(ω0t)u(t) | s/(s2+ω02) | ℝe(s)>0 |
| sen(ω0t)u(t) | ω0/(s2+ω02) | ℝe(s)>0 |
| e-atcos(ω0t)u(t) | (s+a)/((s+a)2+ω02) | ℝe(s) > -a |
| e-atsen(ω0t)u(t) | ω0/((s+a)2+ω02) | ℝe(s) > -a |
Tabla de Propiedades de la Transformada de Laplace
Junto con la Tabla 1 de Transformadas de señales típicas, el análisis requiere del conocimiento de un conjunto de propiedades de la Transformada de Laplace que permitan transformar operaciones complejas en el dominio del tiempo en una serie de operaciones básicas en el dominio transformado, facilitando así la solución del problema. La Tabla 2 presenta un compendio de las propiedades fundamentales de la Transformada de Laplace. En la notación utilizada en la Tabla 2 se cumple que σ , β , s0 son constantes complejas mientras que a , t0 son constantes reales:
\boldsymbol \sigma ,\boldsymbol \beta ,\boldsymbol s_0 \in {\mathbb{C}}\boldsymbol a,\boldsymbol t_0 \in {\mathbb{R}}| Propiedad | Señal Temporal | Transformada de Laplace | ROC |
| x(t) x1(t) x2(t) | X(s) X1(s) X2(s) | R R1 R2 | |
| Linealidad | σ.x1(t)+β.x2(t) | σ.X1(s)+β.X2(s) | Al menos, R1 ∩ R2 |
| Desplazamiento temporal | x(t-t0) | e -st0.X(s) | R |
| Desplazamiento en s | e -ts0.x(t) | X(s-s0) | R+ℝe(s0) |
| Escalado temporal | x(at) | (1/|a|).X(s/a) | a.R |
| Convolución temporal | x1(t)∗x2(t) | X1(s).X2(s) | Al menos, R1 ∩ R2 |
| Derivación temporal | dx(t)/dt | s.X(s) | Al menos, R |
| Derivación en el dominio s | -tx(t) | dX(s)/ds | R |
| Integración temporal | ∫x(t)dt | (1/s).X(s) | Al menos, R ∩ {ℝe(s) >0} |
Se suman a la tabla anterior dos teoremnas que demostrarán ser de gran utilidad en la resolución de problemas, son El Teorema del valor inicial y el Teorema del valor final:
Teorema del valor inicial
Si se cumple que x(t)=0 para t<0, y se cumple además que x(t) no presenta discontinuidades (tipo Delta de Dirac) o singularidades de orden superior en t=0, entonces se cumple que:
\boldsymbol x(0^+) = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol s\rightarrow \mathbf \infty}\boldsymbol s\boldsymbol X(\boldsymbol s)Teorema del valor final
Si se cumple que x(t)=0 para t<0, y se cumple además que x(t) presenta un límite finito cuando t → ∞, entonces se cumple que:
\mathop{\mathbf l\mathbf i\mathbf m}\limits_{\boldsymbol t\rightarrow \mathbf \infty}\boldsymbol x(\boldsymbol t) = \mathop{\mathbf l\mathbf i\mathbf m}\limits_{\mathbf s\rightarrow 0}\boldsymbol s\boldsymbol X\left(\boldsymbol s\right)Te puede interesar:
- Se resuelven ejercicios de Sistemas de Primer y Segundo Orden, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…
Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos. Al suscribirte podrás contar con excelente material para estudiar y superar con éxito las demandas académicas.
Curso relacionado:
Artículos relacionados:
Función de Transferencia – Teoría y práctica.
Relación entrada-salida del sistema – Teoría y práctica.
Diagrama de Bloques – Teoría y práctica.
Linealidad e Invariancia en el tiempo – Teoría y práctica.
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs
