En esta guía PDF se determina el Diagrama de Bloques y la Función de Transferencia mediante la aplicación álgebra de bloques, de los ejercicios que más se utilizan en las clases sistemas de control, señales y sistemas. En total son 10 ejercicios completamente resueltos que involucran el uso de herramientas como álgebra de bloques, Matlab, transformada de Laplace, variables de estado, etc. Es un artículo digital, entregado por email (dademuch@gmail.com) o WhatsApp (+34747458738) una vez recibido el pago.
A continuación, los enunciados de problemas resueltos en esta guía.
1. Obtener la función de transferencia G(s)=Y(s)/R(s) de la Figura 1, por dos métodos: empleando técnicas de reducción por álgebra de bloques y utilizando la fórmula de Mason.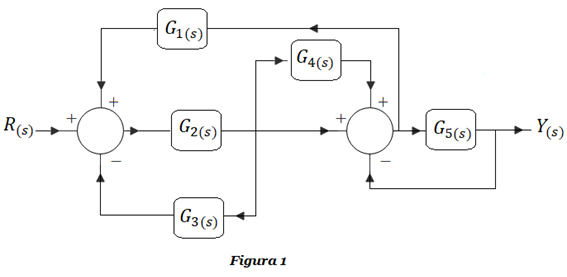 
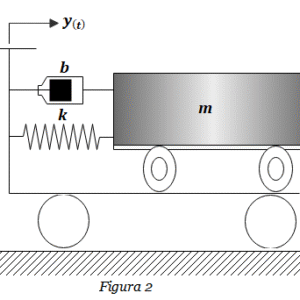
2. Obtener la función de transferencia G(s)=C(s)/R(s) de la Figura 2, por dos métodos: empleando técnicas de reducción por álgebra de bloques y utilizando la fórmula de Mason. 
3. Obtener la función de transferencia G(s)=C(s)/R(s) de la Figura 3, empleando técnicas de reducción por álgebra de bloques. 
4. Obtener la función de transferencia G(s)=Y(s)/R(s) de la Figura 4, empleando técnicas de reducción por álgebra de bloques.
5. Hallar las ecuaciones del sistema de la Figura 7 y representarlo mediante variables de estado. A partir de allí determinar el diagrama de bloques del sistema. Luego, utilizando álgebra de diagrama de bloques, Hallar la función de transferencia X(s)/U(s). Considerar a x(t) como la salida y a u(t) como la entrada. Comprobar el resultado mediante transformada de Laplace. 
6. Hallar las ecuaciones del sistema de la Figura 8. Hallar la representación matricial del sistema (variables de estado). Considere a x1(t) como la salida, y a u(t) como la entrada. Construya el diagrama de bloques del sistema y utilizando álgebra de bloques determinar la función de transferencia X1(s)/U(s).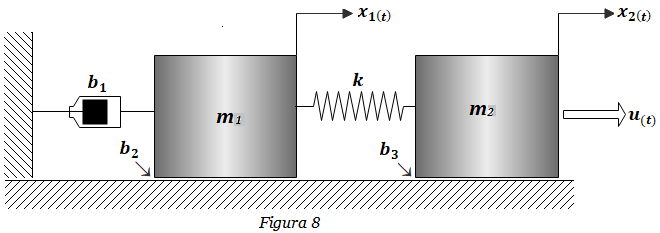 
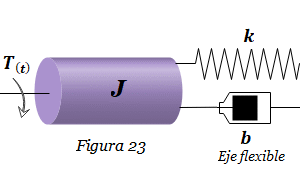
7. Hallar las ecuaciones del sistema de la figura 22. Determinar la función de transferencia X1(s)/U(s). Determinar el diagrama de bloques del sistema a partir de la función de transferencia obtenida. 
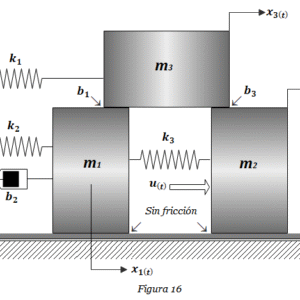
8. Hallar las ecuaciones del Sistema de la Figura 24. Hallar la representación en espacio de estados del sistema, considerando a Θ1(t) como la salida y a T(t) como la entrada. Hallar el diagrama de bloques del sistema y a partir de allí, mediante álgebra de bloques, determinar la función de transferencia Θ1(s)/T(s). 
9. Hallar las ecuaciones del sistema de la Figura 25. Determinar la función de transferencia X1(s)/F(s). Obtener el diagrama de bloques del sistema a partir de la función de transferencia obtenida (Explicar paso a paso). Graficar la respuesta del sistema a una entrada función escalón mediante Matlab. Considerar k1= k2= k3= 1 N/m, b1= b2= b3=1 N-s/m, m1= m2= m3=1 Kg. 
10. Determinar las ecuaciones diferenciales que representan el modelo del sistema de la Figura 75. Utilizar el método de análisis de nodos. Hallar la función de transferencia Vo(s)/V(s). Realice la representación del sistema en diagrama de bloques a partir de la función de transferencia Vo(s)/V(s). Considerar R1=1Ω, R2= R3=1 Ω, L=1 H, C1=C2=1 pF.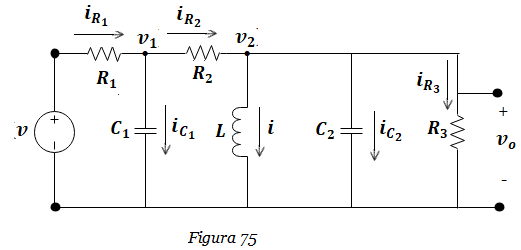 
11. Obtener la función de transferencia Vo(s)/V(s) del sistema eléctrico de la figura 75, a partir del diagrama de bloques del sistema obtenido en el problema 10, utilizando álgebra de bloques. Simular y analizar en Matlab la respuesta del sistema a una entrada escalón unitario.
