Sistema Masa-Resorte-Amortiguador (Rotacional)- Ejercicios Resueltos – Catálogo 4

En esta guía PDF  se determina la Función de Transferencia de los ejercicios que más se utilizan en las clases de sistemas masa-resorte-amortiguador rotacional con engranajes que forman parte de la cátedra de sistemas de control, señales y sistemas, análisis de redes eléctricas con motor DC, sistemas electrónicos en mecatrónica, etc. En total son 10 ejercicios completamente resueltos (distintos al catálogo 3) que involucran el uso de herramientas como álgebra de bloques, Matlab, transformada de Laplace, variables de estado, etc.

A continuación, los enunciados de problemas resueltos en esta guía.

1. Hallar la función de transferencia Θ2(s) /T(s) del Sistema rotacional mostrado en la Figura 34. Utilizar el método que consiste en reflejar el eje de entrada hacia la carga. Considerar k=4 N-m/rad, b=1 N-m-s/rad, J=1 Kg-m2.

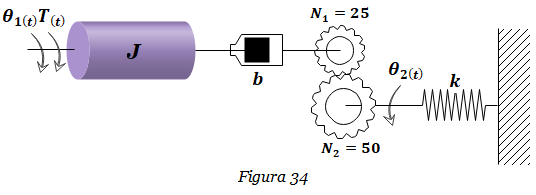
2. Hallar la función de transferencia Θ2(s) /T(s) del Sistema rotacional mostrado en el ejercicio anterior, Figura 34, reflejando las impedancias desde el eje de salida hacia el eje de entrada. Considerar k=4 N-m/rad, b=1 N-m-s/rad, J=1 Kg-m2.

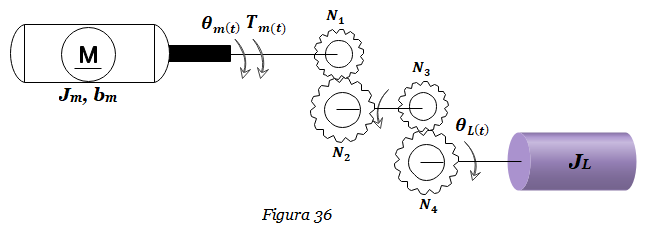
3. Hallar la función de transferencia Θ_L(s) /T_m(s) del Sistema rotacional mostrado en la Figura 36.

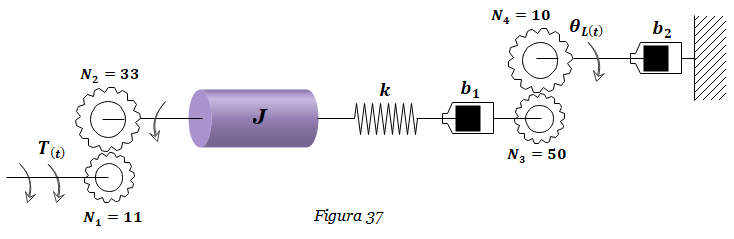
4. Hallar la función de transferencia Θ_L(s) /T_(s) del Sistema mostrado en la Figura 37. Considerar k=3 N-m/rad, b₁=2, b₂=0.04  N-m-s/rad, J=1  Kg-m²

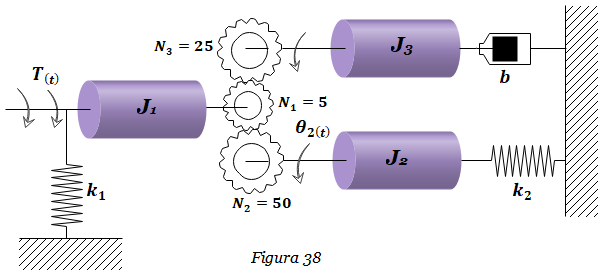
5. Hallar la función de transferencia Θ_2(s) /T_(s) del Sistema mostrado en la Figura 38. Considerar k₁=3, k₂=250 N-m/rad, b=1k N-m-s/rad, J₁=3, J₂=200, J₃=200  Kg-m²

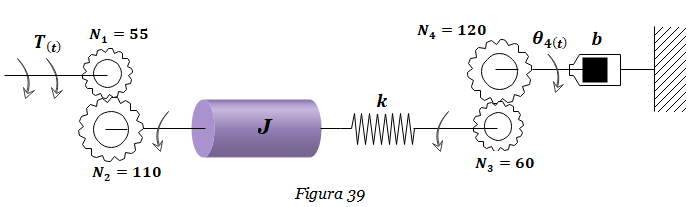
6. Hallar la representación en espacio de estados del Sistema mostrado en la Figura 39 suponiendo que Θ_4(t) es la salida y T_(t) es la entrada. Dibujar el diagrama de bloques del sistema y hallar la función de transferencia Θ_4(s) /T_(s). Considerar k=2 N-m/rad, b=16 N-m-s/rad, J=4  Kg-m²

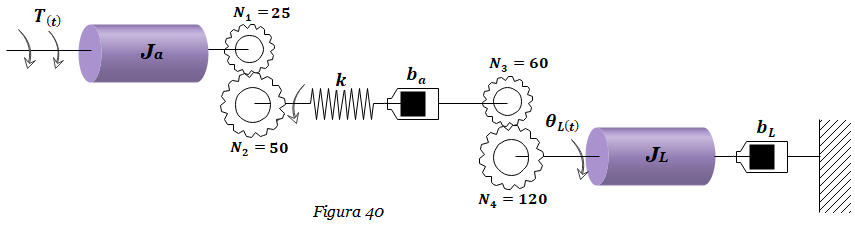
7. Hallar la función de transferencia Θ_L(s) /T_(s) del Sistema mostrado en la Figura 40. Considerar k=3 N-m/rad, ba=2, b_L=4  N-m-s/rad, J_a=1, J_L=8 Kg-m²

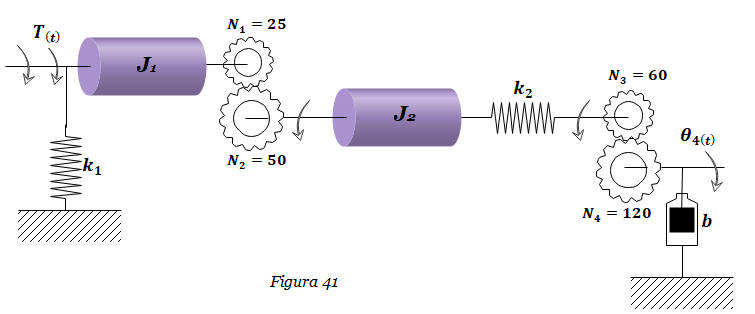
8. Hallar la representación en espacios de estados del Sistema mostrado en la Figura 41, considerando a Θ_4(t) como la salida y a T_(t) como la entrada. Hallar la función de transferencia Θ_4(s) /T_(s). Considerar k₁=1, k₂=2 N-m/rad, b=8, N-m-s/rad, J₁=1, J₂=2 Kg-m²

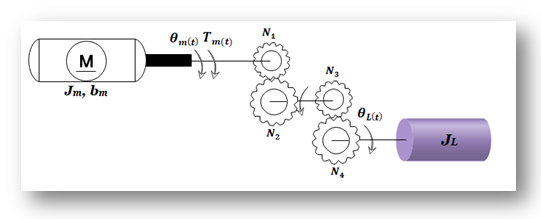
9. Hallar la función de transferencia Θ_L(s) /E_i(s) del Sistema mostrado en la Figura 56.

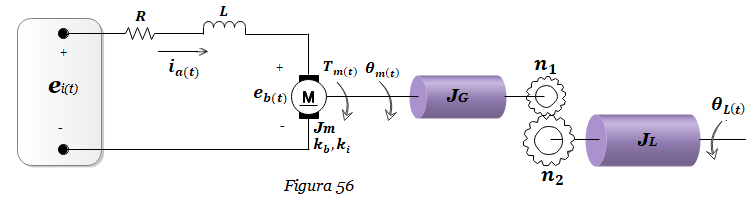
10. Hallar la representación en espacio de estados del Sistema del ejercicio anterior, Figura 56, suponiendo que Θ_L(t) es la salida y que e_i(t) es la entrada. Representar el Sistema mediante un diagrama de bloques.Determinar la f. de transferencia Θ_L(s) /E_i(s).

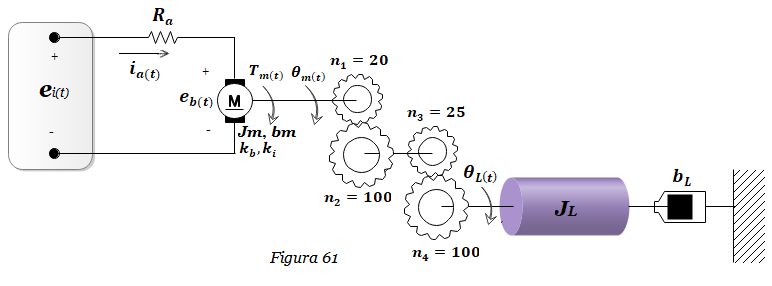
11. Hallar la función de transferencia Θ_L(s) /E_i(s) del Sistema mostrado en la Figura 61. La curva Torque-Velocidad Angular está dada por T_m(t)= -8ω_m(t)+200. Considerar b_m=5, b_L=800  N-m-s/rad, J_m=1,  J_L=400 Kg-m²