Sistema Masa-Resorte-Amortiguador – Ejercicios Resueltos – Catálogo 2

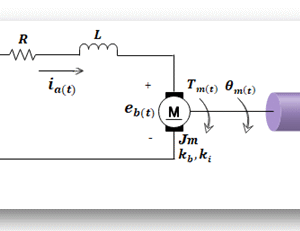
En esta segunda guía PDF  se determina la Función de Transferencia de los ejercicios que más se utilizan en las clases de sistemas masa-resorte-amortiguador que forman parte de la cátedra de sistemas de control, señales y sistemas, análisis de redes eléctricas con motor DC, sistemas electrónicos en mecatrónica, etc. En total son 10 ejercicios completamente resueltos (distintos a los del catálogo 1) que involucran el uso de herramientas como álgebra de bloques, Matlab, transformada de Laplace, variables de estado, etc.

Es un artículo digital, entregado por email (dademuch@gmail.com) o WhatsApp (+34747458738) una vez recibido el pago.

A continuación, los enunciados de problemas resueltos en esta guía.

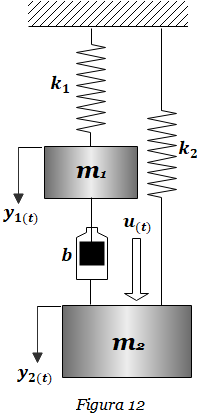
1. Hallar las funciones de transferencia Y_1(s)/U_(s) y Y_2(s)/U_(s) del Sistema que se muestra en la Figura 12.

2. Hallar las funciones de transferencia Y_1(s)/U_(s) y Y_2(s)/U_(s) del Sistema que se muestra en la Figura 13.

3. Hallar las funciones de transferencia X_1(s)/U_(s) y X_2(s)/U_(s) del Sistema mostrado en la Figura 14.

4. Hallar la función de transferencia X_2(s)/U_(s) del Sistema mostrado en la Figura 15. Considerar k₁=1, k₂= 15 N/m, b₁=4, b₂= 16 N-s/m, m₁= 8, m₂=3  Kg.

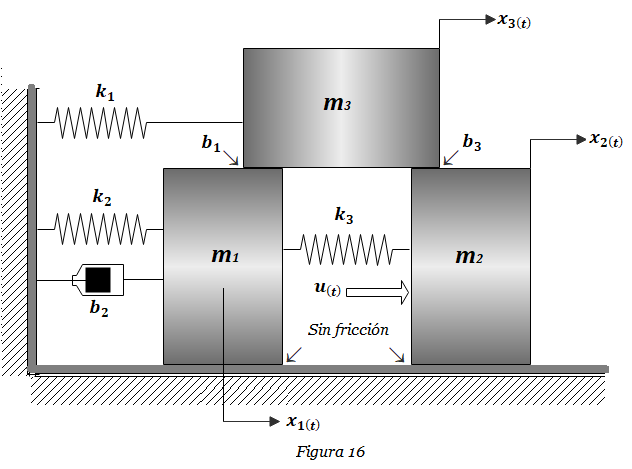
5. Hallar la función de transferencia X_3(s)/U_(s)  del Sistema mostrado en la Figura 16. Considerar k₁=5, k₂= 4. k₃= 4  N/m, b₁=2, b₂= 2, b₃= 3  N-s/m, m₁= 4, m₂=5, m₃=5  Kg.

6. Hallar la función de transferencia X_1(s)/U_(s) del Sistema mostrado en la Figura 17. Considerar k₁=k₂= 1 N/m, b₁= b₂= b₃= 1  N-s/m, m₁= 2, m₂=1, m₃=1  Kg. _{El mismo ejercicio se resuelve con variables de estado en el próximo número.}

7. Hallar el modelo en espacio de estados del Sistema del ejercicio anterior Figura 17, tomando a x_1(t) como la salida y u_(t) como la entrada. Transformar dicho modelo en la función de transferencia X_1(s)/U_(s). Considerar k₁=k₂= 1 N/m, b₁= b₂= b₃= 1  N-s/m, m₁= 2, m₂=1, m₃=1  Kg.

8. Hallar la función de transferencia Y_h(s)/f_up(s) del Sistema de la Figura 19. Considerar k_h=7, k_s=8, k_ave=5  N/m, b_f=3, b_h= 10  N-s/m, m_h=1, m_f=2 Kg.

9. Hallar las funciones de transferencia X_2(s)/U_(s) y X_3(s)/U_(s) del Sistema de la Figura 20. Considerar k₁=1, k₂=2, k₃=3, k₄=4 N/m, b₁=2,b₂= 1,b₃= 3 N-s/m, m₁=2,m₂=1,m₃=3  Kg.

10. Hallar la representación en espacio de estados tomando x_3(t) como salida y u_(t) como entrada, y la función de transferencia X_3(s)/U_(s) del sistema mostrado en la Figura 21. Considerar k=2 N/m, b₁=b₂=b₃=b₄=b₅=1 N-s/m, m₁=2,m₂=1,m₃=1 Kg.

11. Determinar la función de transferencia y el diagrama de bloques del sistema de la figura 22: