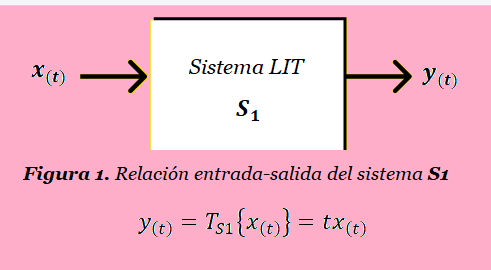
Las Propiedades de los Sistemas más relevantes son las siguientes: Linealidad, Invariancia en el tiempo, Causalidad, Estabilidad y Memoria. La mayoría de los ejercicios relacionados con este tema requieren demostrar las propiedades de los sistemas, para lo cual es necesario aplicar la definición de cada propiedad a la relación entrada-salida del sistema. En especial, interesan los sistemas que cumplen con las propiedades de Linealidad e Invariancia en el tiempo (Sistemas LIT), porque dichos sistemas son de gran importancia para el análisis de señales y sistemas en general. La Figura 1 ilustra la relación entrada-salida del sistema LIT denominado S1.
Propiedades de los sistemas
Las propiedades que vamos a definir y luego demostrar son las siguientes:
Para demostrar las propiedades de los sistemas es necesario aplicar la definición de cada propiedad a la relación entrada-salida del sistema.
Relación entrada-salida del sistema.
La relación entrada-salida de un sistema es aquella expresión algebraica, por lo general una Ecuación Diferencial del Sistema (EDS), que nos permite conocer la señal de salida y(t) en función de la señal de entrada x(t).
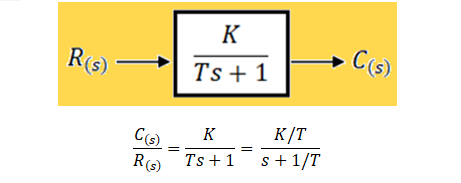
Por ejemplo, un sistema de primer orden es aquel cuya relación entrada-salida en el dominio del tiempo, está definida por una ecuación diferencial de primer orden del tipo:
\frac{\boldsymbol d\boldsymbol y(\boldsymbol t)}{\boldsymbol d\boldsymbol t} + \boldsymbol a_0\boldsymbol y(\boldsymbol t) = \frac{\boldsymbol d\boldsymbol x\left(\boldsymbol t\right)}{\boldsymbol d\boldsymbol t} + \boldsymbol b_0\boldsymbol x\left(\boldsymbol t\right);\ para\ cada\ t\text{∈}\text{R}La Ecuación Diferencial del Sistema (EDS) es un modelo dinámico que establece una restricción fundamental sobre ciertas combinaciones de la entrada, la salida y algunas derivadas de ambas señales.
La relación entrada-salida de un sistema puede ser una simple expresión algebraica que nos permita directamente determinar la salida en función de la entrada. Sea la siguiente relación entrada-salida del sistema S1:
\boldsymbol y(\boldsymbol t) = \boldsymbol t\boldsymbol x(\boldsymbol t)
Dada una señal x(t) cualquiera, utilizando la ecuación anterior podemos conocer la expresión de salida y(t) del sistema S1.
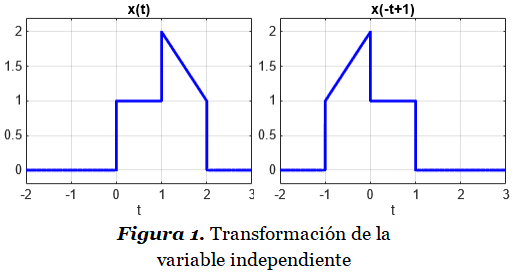
Si la entrada x(t) al sistema S1 es la siguiente:
x\left(t\right) = u(t - 1) - u(t - 3)
Entonces la salida y(t) del sistema S1 es:
y(t) = tx(t)\ \ \rightarrow\ \ \boldsymbol y\left(\boldsymbol t\right) = \boldsymbol t(\boldsymbol u(\boldsymbol t - 1) - \boldsymbol u(\boldsymbol t - 3))
Más adelante utilizaremos el sistema S1 para demostrar el cumplimiento de las propiedades de los sistemas. Además, utilizaremos de vez en cuando la siguiente notación, ecuación (1), cuando nos refiramos a la relación entrada-salida en términos generales:
Relación\ entrada-salida:\ \ \ \ \ \boldsymbol y(\boldsymbol t) = \boldsymbol T_{\boldsymbol s}\left\{\boldsymbol x(\boldsymbol t)\right\}\ \ \ \ \ (1)La Ts de la ecuación (1) significa «la acción del sistema S sobre la entrada…». En este caso Ts {x(t) } significa «la acción del sistema S sobre la entrada x(t) «
En el caso del tiempo discreto:
Relación\ entrada-salida:\ \ \ \ \ \boldsymbol y[\boldsymbol n] = \boldsymbol T_{\boldsymbol s}\left\{\boldsymbol x[\boldsymbol n]\right\}\ \ \ \ \ (2)Para ver como demostrar las propiedades de los sistemas observa los ejercicios resueltos.
Propiedad de linealidad.
Definición: Un sistema continuo o discreto es lineal si cumple con la propiedad de superposición.
En consecuencia, si la entrada al sistema está compuesto por la suma de varias señales, entonces la salida estará compuesta por la suma de las respuestas del sistema a cada una de esas señales de entrada. Esta situación se puede resumir de la manera siguiente. Supongamos que para un sistema S cualquiera, llamamos x(t) a su señal de entrada y y(t) a su señal de salida. Si se presentan dos señales por separado en la entrada del sistema S serán llamadas x1(t) y x2(t), por lo tanto las salidas a cada una de esas entradas serán llamadas y1(t) y y2(t). Entonces, el sistema S será lineal si:
- La salida del sistema es y(t) =y1(t) + y2(t) cuando la entrada al sistema es x(t)=x1(t) + x2(t). Esta propiedad se denomina a su vez aditividad;
- La salida del sistema es y(t) =α.y1(t) +ß.y2(t) cuando la entrada al sistema es x(t)=α.x1(t) +ß.x2(t). Esta propiedad se denomina escalamiento u homogeneidad ; donde las letras α(alfa) y ß(beta) son números reales o complejos cualquiera, y se utilizan para representar la posible combinación lineal de las entradas al sistema.
Un tratamiento más riguroso se presenta en el siguiente video, que incluye el tiempo continuo y el tiempo discreto:
Para ver como demostrar la propiedad de linealidad de los sistemas observa los ejercicios resueltos.
Invariancia en el tiempo.
Definición: Un sistema continuo o discreto es invariante en el tiempo si ante un desplazamiento temporal (horizontal) de la entrada, el sistema preserva su salida, la cual sufre un desplazamiento temporal equivalente.
Es decir, si la salida del sistema S continuo es y(t) cuando la entrada es x(t), el sistema S es invariante en el tiempo si su salida es y(t-t0) cuando la entrada es x(t-t0).
De forma paralela, si la salida del sistema S discreto es y[n] cuando la entrada es x[n], el sistema S es invariante en el tiempo si su salida es y[n-n0] cuando la entrada es x[n-n0].
Utilizando las ecuaciones (1) y (2) podemos afirmar que el sistema S es invariante en el tiempo si se cumple lo siguiente. En el caso del tiempo continuo:
\boldsymbol y(\boldsymbol t) = \boldsymbol T_{\boldsymbol s}\left\{\boldsymbol x(\boldsymbol t)\right\}\Leftrightarrow \boldsymbol y\left(\boldsymbol t - \boldsymbol t_0\right) = \boldsymbol T_{\boldsymbol s}\left\{\boldsymbol x\left(\boldsymbol t - \boldsymbol t_0\right)\right\}En el caso del tiempo discreto:
\boldsymbol y\left[\boldsymbol n\right] = \boldsymbol T_{\boldsymbol s}\left\{\boldsymbol x\left[\boldsymbol n\right]\right\}\Leftrightarrow \boldsymbol y\left[\boldsymbol n - \boldsymbol n_0\right] = \boldsymbol T_{\boldsymbol s}\left\{\boldsymbol x\left[\boldsymbol n - \boldsymbol n_0\right]\right\}Para ver como demostrar la propiedad de invariancia en el tiempo de los sistemas observa los ejercicios resueltos.
Sistemas con memoria
Definición: Un sistema continuo o discreto tiene memoria si posee la capacidad de almacenar información de la entrada de tiempo anterior al tiempo presente, y luego utilizar esa información para calcular la salida en el tiempo presente. En otras palabras, el sistema tiene memoria si al observar su relación entrada-salida en el tiempo t encontramos elementos que utilizan valores anteriores a ese tiempo t.
Alternativamente, un sistema no tiene memoria si el valor de su salida en un tiempo t depende solamente de los valores de la entrada en ese mismo instante t.
Si la salida del sistema S continuo es y(t) cuando la entrada es x(t), la siguiente lista hace un resumen de lo dicho hasta ahora:
- El sistema S tiene memoria si y solo si el valor de la salida y(t) en algún instante de tiempo t depende de algún valor de la entrada x(t) ubicado antes de dicho instante t.
- El sistema S no tiene memoria si y solo si el valor de la salida y(t) en algún instante de tiempo t nunca depende de algún valor de la entrada x(t) ubicado antes de dicho instante t.
- Se dice que el sistema S es instantáneo si y solo si el valor de la salida y(t) solo depende del valor de la entrada x(t) ubicado en ese mismo instante t.
Para ver como demostrar la propiedad de memoria de los sistemas observa los ejercicios resueltos.
Estabilidad
Definición: Un sistema continuo o discreto es estable si genera una salida acotada cuando la entrada está acotada. En otras palabras, el sistema es inestable si una entrada pequeña produce una salida divergente.
Es decir, si la salida del sistema S continuo es y(t) cuando la entrada es x(t), el sistema S es estable si su salida está acotada en amplitud cuando su entrada está también acotada en amplitud. Esta situación se puede expresar matemáticamente mediante:
\left|\boldsymbol x(\boldsymbol t)\right| \leq \boldsymbol A\Rightarrow \left|\boldsymbol y\left(\boldsymbol t\right)\right| \leq \boldsymbol B\boldsymbol ;\ \ \ \ \boldsymbol A\boldsymbol \ y\ \boldsymbol B \in {\mathbb{R}}En el caso del tiempo discreto:
\left|\boldsymbol x[\boldsymbol n]\right| \leq \boldsymbol A\Rightarrow \left|\boldsymbol y\left[\boldsymbol n\right]\right| \leq \boldsymbol B\boldsymbol ;\ \ \ \ \boldsymbol A\boldsymbol \ y\ \boldsymbol B \in {\mathbb{R}}Las letras A y B representan valores reales y finitos de amplitud.
Para ver como demostrar la propiedad de estabilidad de los sistemas observa los ejercicios resueltos.
Causalidad
Definición: Un sistema continuo o discreto es causal si genera una salida que depende solo de valores de la entrada ubicados en el presente y/o en el pasado.
Es decir, si la salida del sistema S continuo es y(t) cuando la entrada es x(t), la siguiente lista hace un resumen de la propiedad de causalidad de dicho sistema:
- El sistema S es causal si y solo si el valor de la salida y(t) en algún instante de tiempo t depende de algún valor de la entrada x(t) ubicado en dicho instante t o antes de dicho instante t.
- El sistema S no es causal si y solo si el valor de la salida y(t) en algún instante de tiempo t depende de algún valor de la entrada x(t) ubicado después de dicho instante t.
Para ver como demostrar la propiedad de causalidad de los sistemas observa los ejercicios resueltos.
Ejercicios resueltos de Propiedades de los Sistemas
El objetivo en los siguientes ejercicios es demostrar las propiedades de los sistemas utilizando la relación entrada-salida de cada sistema y utilizando la definición de cada propiedad expuesta anteriormente. Se demuestran las propiedades de los sistemas mediante un método paso a paso, basado en las mejores prácticas de la teoría clásica de señales y sistemas.
Ejercicio SS1-2: Justifique si los siguientes sistemas, caracterizados por su relación entrada-salida, son lineales, invariantes en el tiempo, con memoria, causales y/o estables:
Sistema\ 1:\ \ \boldsymbol y(\boldsymbol t) = \boldsymbol t\boldsymbol x(\boldsymbol t)
Sistema\ 2:\ \ \boldsymbol y(\boldsymbol t) = 2\boldsymbol x(\boldsymbol t/ 3)
Sistema\ 3:\ \ \boldsymbol y[\boldsymbol n] = \boldsymbol x[\boldsymbol n] + 1
Encontrarás la solución al ejercicio SS1-2 en el siguiente link: SOLUCIÓN Ejercicio SS1-2.
Te puede interesar:
- Se resuelven ejercicios de Señales y Sistemas 1 y 2, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…
Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos. Al suscribirte podrás contar con excelente material para estudiar y superar con éxito las demandas académicas.
Curso relacionado:
Artículos relacionados:
- Función de Transferencia – S. Mecánico – Ejercicio resuelto 1
- Función de Transferencia – S. Mecánico – Ejercicio resuelto 2
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs