La relación entrada-salida de un sistema es aquella expresión algebraica, por lo general una Ecuación Diferencial del Sistema (EDS), que nos permite conocer la señal de salida y(t) en función de la señal de entrada x(t).
Por ejemplo, un sistema de primer orden es aquel cuya relación entrada-salida en el dominio del tiempo, está definida por una ecuación diferencial de primer orden del tipo:
\frac{\boldsymbol d\boldsymbol y(\boldsymbol t)}{\boldsymbol d\boldsymbol t} + \boldsymbol a_0\boldsymbol y(\boldsymbol t) = \frac{\boldsymbol d\boldsymbol x\left(\boldsymbol t\right)}{\boldsymbol d\boldsymbol t} + \boldsymbol b_0\boldsymbol x\left(\boldsymbol t\right);\ para\ cada\ t\text{∈}\text{R}La Ecuación Diferencial del Sistema (EDS) es un modelo dinámico que establece una restricción fundamental sobre ciertas combinaciones de la entrada, la salida y algunas derivadas de ambas señales.
La relación entrada-salida de un sistema puede ser una simple expresión algebraica que nos permita directamente determinar la salida en función de la entrada. Sea la siguiente relación entrada-salida del sistema S1:
\boldsymbol y(\boldsymbol t) = \boldsymbol t\boldsymbol x(\boldsymbol t)
Dada una señal x(t) cualquiera, utilizando la ecuación anterior podemos conocer la expresión de salida y(t) del sistema S1.
Si la entrada x(t) al sistema S1 es la siguiente:
x\left(t\right) = u(t - 1) - u(t - 3)
Entonces la salida y(t) del sistema S1 es:
y(t) = tx(t)\ \ \rightarrow\ \ \boldsymbol y\left(\boldsymbol t\right) = \boldsymbol t(\boldsymbol u(\boldsymbol t - 1) - \boldsymbol u(\boldsymbol t - 3))
Más adelante utilizaremos el sistema S1 para demostrar el cumplimiento de las propiedades de los sistemas. Además, utilizaremos de vez en cuando la siguiente notación, ecuación (1), cuando nos refiramos a la relación entrada-salida en términos generales:
Relación\ entrada-salida:\ \ \ \ \ \boldsymbol y(\boldsymbol t) = \boldsymbol T_{\boldsymbol s}\left\{\boldsymbol x(\boldsymbol t)\right\}\ \ \ \ \ (1)La Ts de la ecuación (1) significa «la acción del sistema S sobre la entrada…». En este caso Ts {x(t) } significa «la acción del sistema S sobre la entrada x(t) «
En el caso del tiempo discreto:
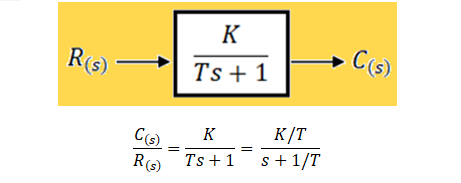
Relación\ entrada-salida:\ \ \ \ \ \boldsymbol y[\boldsymbol n] = \boldsymbol T_{\boldsymbol s}\left\{\boldsymbol x[\boldsymbol n]\right\}\ \ \ \ \ (2)La Función de Transferencia de un sistema LIT analógico viene a ser el elemento que conecta la relación entrada-salida de dicho sistema con su respuesta impulsional h(t). Es decir, podemos obtener una a partir de la otra mediante el siguiente proceso:
- Si queremos obtener h(t) para un sistema en particular del cual sólo poseemos un esquema gráfico, debemos obtener en primer lugar la relación entrada-salida del sistema utilizando leyes de la física (ver ejemplos en el siguiente apartado), luego aplicar la transforma de Laplace a la EDS obtenida, despejar la función de transferencia H(s) y finalmente aplicar la antitransformada de Laplace, lo que nos proporciona la expresión matemática para h(t).
- Si por el contrario, queremos obtener la EDS del sistema a partir de su respuesta impulsional h(t), aplicaremos la transforma de Laplace a la ecuación de h(t), es decir, obtenemos la Función de Transferencia H(s), y con ésta última podemos obtener la EDS del sistema aplicando las propiedades de la Transformada de Laplace.
e puede interesar:
- Se resuelven ejercicios de Determinar la Función de Transferencia, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…
Artículos relacionados:
- Función de Transferencia – S. Mecánico – Ejercicio resuelto 1
- Función de Transferencia – S. Mecánico – Ejercicio resuelto 2
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs
