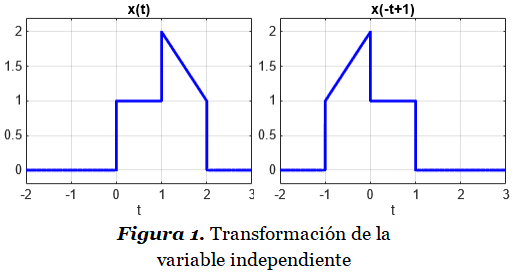
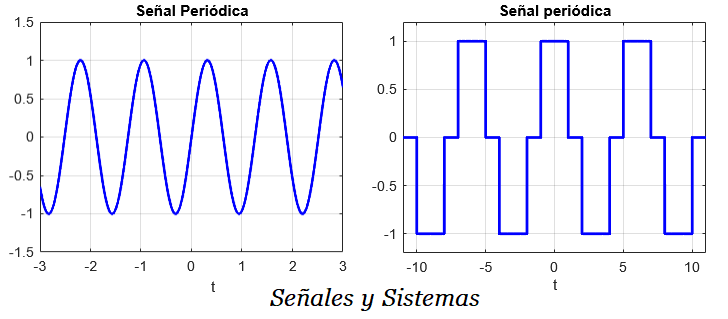
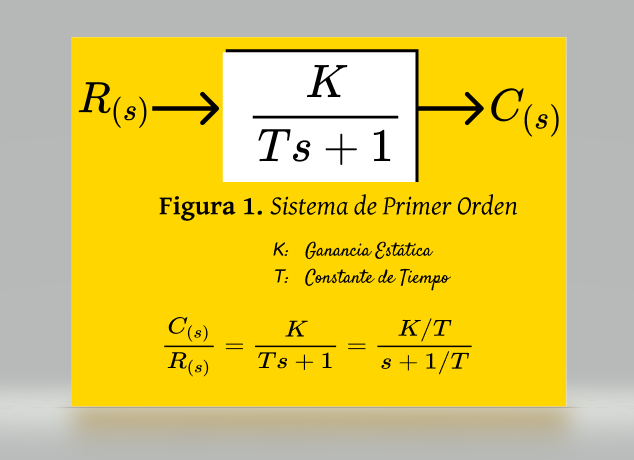
Un Sistema de Primer Orden se representa generalmente mediante el Diagrama de Bloques y La Función de Transferencia de la Figura 1. La Ganancia Estática K y La Constante de Tiempo T son los parámetros que definen el comportamiento de un Sistema de Primer Orden.
¿Qué es un sistema de primer orden?
Un sistema de primer orden es aquel cuya relación entrada salida en el dominio del tiempo, está definida por una ecuación diferencial de primer orden del tipo:
\frac{\boldsymbol d\boldsymbol y(\boldsymbol t)}{\boldsymbol d\boldsymbol t} + \boldsymbol a_0\boldsymbol y(\boldsymbol t) = \boldsymbol b_0\boldsymbol x\left(\boldsymbol t\right);\ para\ cada\ t\ \text{∈}\ \text{R}\ \ (1)La ecuación (1) es la Ecuación Diferencial del Sistema (EDS), un modelo dinámico que establece una restricción fundamental sobre ciertas combinaciones de la entrada, la salida y algunas derivadas de ambas señales.
Aplicando La Transformada de Laplace a la ecuación (1), podemos obtener La Función de Transferencia G(s) del Sistema:
\boldsymbol G(\boldsymbol s) =\frac{\boldsymbol Y(\boldsymbol s)}{\boldsymbol X(\boldsymbol s)} \boldsymbol G(\boldsymbol s) = \frac{\boldsymbol b_0}{\boldsymbol s + \boldsymbol a_0}Reordenando y renombrando las constantes de la ecuación anterior de la siguiente manera:
\boldsymbol G(\boldsymbol s) = \frac{\frac{\boldsymbol b_0}{\boldsymbol a_0}}{\frac{\boldsymbol s}{\boldsymbol a_0} + 1}\rightarrow \frac{\boldsymbol b_0}{\boldsymbol a_0} = K;\frac{1}{\boldsymbol a_0} = TObtenemos la forma adimensional o forma estándar de La Función de Transferencia de un Sistema de Primer Orden:
\boldsymbol G(\boldsymbol s) = \frac{\boldsymbol K}{\boldsymbol T\boldsymbol s + 1} ;\ \ \ (2)dónde \ \ \ \ \boldsymbol K: Ganancia \ Estática;\ \ \ \ \boldsymbol T:Constante\ de\ tiempo
La Ganancia Estática K y La Constante de Tiempo T son los parámetros que definen el comportamiento de un Sistema de Primer Orden.
La respuesta en el tiempo.
El método más utilizado para estudiar el comportamiento de los sistemas de 1er orden consiste en someter dicho sistema a un conjunto de entradas típicas: el impulso, el escalón unitario, la rampa o una señal sinusoidal.
La simulación de la salida del sistema a cualquiera de las entradas típicas nos permite obtener los parámetros del sistema definidos en la ecuación (2).
Una vez obtenida la Función de Transferencia, ecuación (2), aplicando el método de fracciones parciales y luego la transformada inversa de Laplace, podemos determinar la respuesta en el tiempo. Es decir, la ecuación de la salida y(t) del sistema.
En el próximo ejercicio solo disponemos de la gráfica de la señal de salida y(t) cuando la entrada x(t) del sistema es una señal escalón. Exponiendo los conceptos teóricos para Sistemas de Primer Orden y aplicando dichos conceptos a la gráfica de la señal de salida, podremos calcular el valor de los parámetros que definen el sistema.
En este curso aprenderás:
- ¿Qué es la Ganancia Estática? ¿Cómo se calcula?
- ¿Que´es la Constante de Tiempo?¿Cómo se calcula?
- ¿Qué es el tiempo de asentamiento?¿Cómo se calcula?
- ¿Cómo determinar la Función de Transferencia (FT) del Sistema?
- Analizar la Gráfica de la Respuesta al Escalón Unitario
- ¿Cuál es la expresión matemática de la salida del sistema en el tiempo? (a la entrada impulsiva, escalón y rampa unitaria)
- ¿Cuál es la velocidad de la respuesta de la salida del sistema en t=0 s?
- ¿Cómo determinar la Ecuación Diferencial del Sistema?
- Método de descomposición en fracciones parciales.
- Simular en Matlab la respuesta en el tiempo del sistema para comprobar los resultados.
- Graficar la respuesta impulsional, la respuesta a la entrada escalón unitario y a la entrada rampa unitaria.
- Código de Matlab de las Gráficas.
- Todo esto en la SOLUCIÓN al ejercicio S1O-1.
Ejercicios de sistemas de primer orden
Ejercicio S1O-1: Supongamos que disponemos de un sistema de primer orden llamado S1, cuya entrada es la señal x(t) y la salida es la señal y(t). La Gráfica 1 muestra la respuesta y(t) del sistema S1 para una entrada x(t) escalón de amplitud A=2.
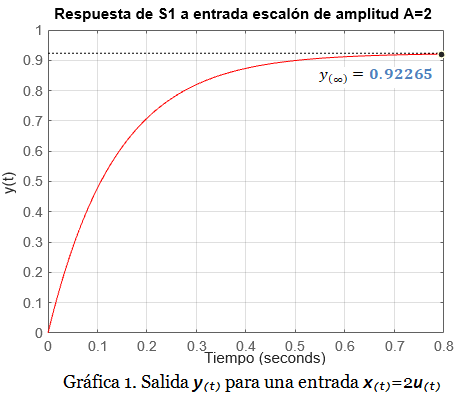
Con respecto a la Gráfica 1 responde a las siguientes preguntas:
- ¿Qué es la ganancia estática? ¿Cuál es su valor para el sistema S1?
- ¿Qué es la constante de tiempo? ¿Cuál es su valor para el sistema S1?
- ¿Qué es el tiempo de asentamiento? ¿Cuál es su valor para el sistema S1?
- ¿Cuál es la función de transferencia y la ecuación diferencial del sistema S1?
- ¿Cuál es la expresión matemática de y(t), la salida del sistema S1 en el tiempo? ¿y para una entrada escalón unitario?
- Simular en Matlab la solución y comparar con la Gráfica 1. Uso de los comandos damp y stepinfo para determinar los valores de los parámetros en la simulación.
- ¿Cuál es la velocidad de la respuesta y(t) en t=0 s?
- Determinar y Graficar la respuesta impulsional del sistema S1
- Determinar y Graficar la respuesta a la entrada rampa unitaria del sistema S1
Encontrarás la solución al ejercicio S1O-1 en el siguiente link: SOLUCIÓN Ejercicio S1O-1.
Procedimiento:
- Antes de resolver cada pregunta se hace una definición teórica y demostración matemática de cada concepto.
- Solo disponemos de la gráfica de la señal y(t) cuando la entrada x(t) del sistema es una señal típica (escalón). Aplicando conceptos teóricos a dicha gráfica procedemos a calcular el valor de los parámetros que definen el sistema de primer orden (ganancia estática y constante de tiempo), y determinar la Función de Transferencia, la cual a su vez nos permitirá determinar la salida y(t) para cualquier entrada x(t).
- Para obtener la Ecuación Diferencial del Sistema (EDS) S1, aplicamos álgebra (reordenamos su FT) y antitransformada de Laplace.
- La solución escrita del Examen 10-1 es excelente herramienta para comprender los conceptos básicos y fundamentales de Sistemas de Primer Orden. Los ejemplos en muchos casos explican mucho mejor que la teoría, la idea que se quiere transmitir.
- Aplicaremos las técnicas de análisis de libros de texto más utilizados: Ogata, Kuo, Oppenheim, etc.
Te puede interesar:
- Se resuelven ejercicios de Sistemas de Primer y Segundo Orden, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…
Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos. Al suscribirte podrás contar con excelente material para estudiar y superar con éxito las demandas académicas.
Curso relacionado:
Artículos relacionados:
Función de Transferencia – Teoría y práctica.
Relación entrada-salida del sistema – Teoría y práctica.
Diagrama de Bloques – Teoría y práctica.
Linealidad e Invariancia en el tiempo – Teoría y práctica.
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs