Ejercicio S10-1
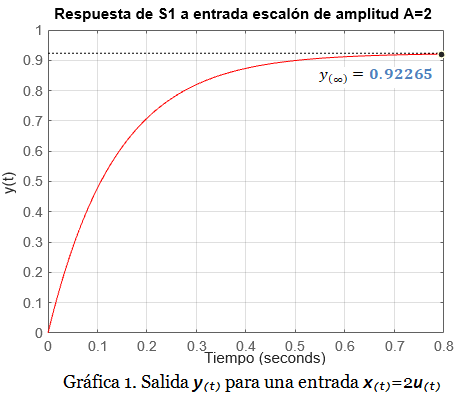
Supongamos que disponemos de un sistema de primer orden llamado S1, cuya entrada es la señal x(t) y la salida es la señal y(t). La Gráfica 1 muestra la respuesta y(t) del sistema S1 para una entrada x(t) escalón de amplitud A=2.
En este artículo se responde a las siguientes preguntas:
- ¿Qué es la ganancia estática? ¿Cuál es su valor para el sistema S1?
- ¿Qué es la constante de tiempo? ¿Cuál es su valor para el sistema S1?
- ¿Qué es el tiempo de asentamiento? ¿Cuál es su valor para el sistema S1?
- ¿Cuál es la función de transferencia y la ecuación diferencial del sistema S1?
- ¿Cuál es la expresión matemática de y(t), la salida del sistema S1 en el tiempo? ¿y para una entrada escalón unitario?
- ¿Cuál es la velocidad de la respuesta y(t) en t=0 s?
- Simular en Matlab la solución y comparar con la Gráfica 1.
- Determinar y Graficar la respuesta impulsional del sistema S1
- Determinar y Graficar la respuesta a la entrada rampa unitaria del sistema S1
¿Qué es la ganancia estática? ¿Cuál es su valor para el sistema S1?
Considerando la respuesta de un sistema lineal estable de primer orden a una entrada escalón de amplitud A, vamos a demostrar que: “la ganancia estática K del sistema es la relación entre el valor de estabilización de la señal de salida y la amplitud A de la señal de entrada aplicada.” En consecuencia:
\boldsymbol K = \frac{y(\infty )}{A}Dónde:
:respuesta en el tiempo a la entrada escalón de amplitud A: valor de la salida en estado estable
: entrada escalón de amplitud A
Demostración:
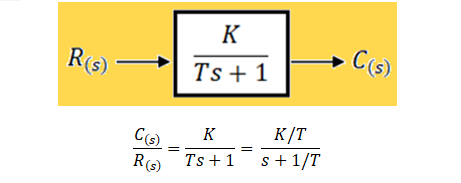
La función de transferencia normalizada de un sistema de 1er orden es la ecuación (1):
\frac{Y(s)}{X(s)} = \frac{\boldsymbol K}{\boldsymbol Ts + 1};\ \ \ \ \ (1)Dónde:
: constante de tiempo: ganancia estática
Se aplica como señal de entrada al sistema de 1er orden, un escalón de amplitud A.
La transformada de Laplace de un escalón de amplitud A es:
x(t) = \boldsymbol Au(t)\mathop{\rightarrow}\limits^{{\mathcal{L}}}X(s) = \frac{\boldsymbol A}{s}; \ \ \ \ \ (2)Sustituyendo la ecuación (2) en la función de transferencia de la ecuación (1) podemos determinar directamente la expresión de Y(s), la salida del sistema en el dominio transformado:
Aplicando el teorema del valor final podemos determinar la expresión para la salida y(t) en estado estable (cuando t tiende a infinito):
Despejando K del resultado anterior, obtenemos que:
\boldsymbol K = \frac{y(\infty )}{A}Observación: para conocer el valor de la ganancia estática en un sistema de primer orden, es necesario aplicar una entrada escalón. Cuando la entrada es el escalón unitario (señal escalón de amplitud A=1), el valor de la ganancia estática K de ese sistema coincide con el valor de la salida en estado estable:
\boldsymbol K = \frac{y(\infty )}{A} = \frac{y(\infty )}{1}\rightarrow \boldsymbol K = \boldsymbol y\left(\mathbf \infty \right)¿Cuál es el valor de la ganancia estática para el sistema S1?

De acuerdo con la Gráfica 1, el valor de la salida en estado estable es:
La entrada es un escalón de amplitud A=2. Por lo tanto, utilizando la ecuación (3):
La ganancia estática K tiene una valor de:
\boldsymbol K = 0.46133
¿Qué es la constante de tiempo? ¿Cuál es su valor para el sistema S1?
Considerando la respuesta de un sistema lineal estable de primer orden a una entrada escalón de amplitud A: «la constante de tiempo T es el tiempo que tarda la señal de salida y(t) en alcanzar el 63.2% de su valor de estabilización». Mientras más pequeña es la constante de tiempo T, más rápido es el sistema.
Un dato importante es que la constante de tiempo del sistema de primer orden no depende de la amplitud de la señal de entrada. Si utilizamos un escalón unitario como señal de entrada a un sistema representado por la siguiente Función de Transferencia típica de un sistema de primer grado, obtendríamos la siguiente respuesta (Gráfica 1.1):
\frac{C(s)}{R(s)} = \frac{\boldsymbol1}{\boldsymbol Ts + 1};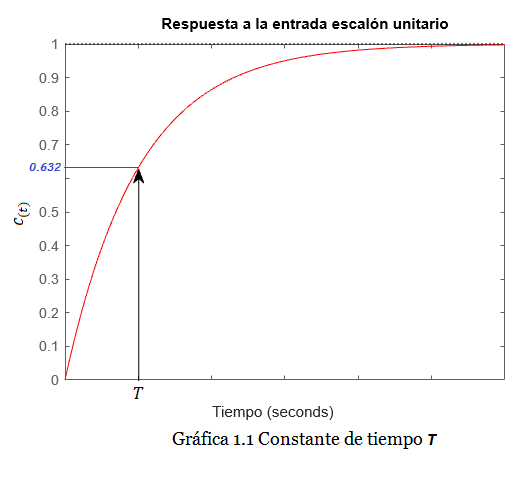
Observación: es necesario resaltar que la definición de la constante de tiempo que hemos dado (el tiempo que tarda la señal de salida en alcanzar el 63.2% de su valor de estabilización) se refiere a la respuesta del sistema a una entrada escalón (step response).
¿Cuál es el valor de la constante de tiempo para el sistema S1?
Utilizando nuevamente la Gráfica 1, podemos calcular el 63.2% del valor de la salida en estado estable mediante:
y(\infty ) \times \frac{6.32}{100} = 0.92265 \times \left(0.632\right) = 0.58311La constante de tiempo T para el sistema S1 es el tiempo en que la curva alcanza el valor de 0.58. Trazando una flecha en la Gráfica 1 que intercepte el eje de las abscisas cuando la curva alcanza el valor de 0.58, podemos determinar de manera aproximada la constante de tiempo T:
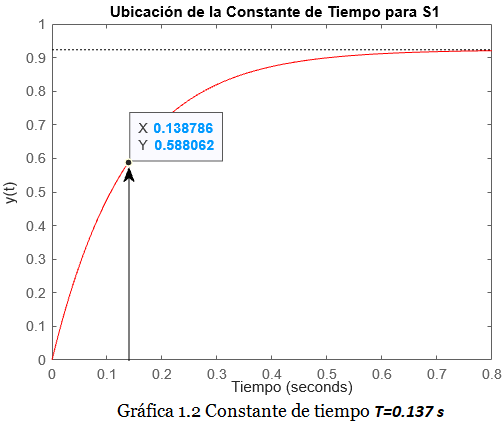
Por lo tanto, la constante de tiempo T tiene un valor aproximado de:
\boldsymbol T = 0.137\boldsymbol \ \ s
¿Qué es el tiempo de asentamiento? ¿Cuál es su valor para el sistema S1?
Definición: “el tiempo de asentamiento ts se define como el tiempo que tarda la señal de salida en alcanzar y permanecer dentro del 2% de su valor de estabilización (criterio del 2%)”. En un sistema de primer grado el tiempo de asentamiento ocurre para t=4T (cuatro veces la Constante de Tiempo T).
Una vez más, este concepto está relacionado con la respuesta del sistema a la entrada escalón. Por lo general se utiliza el escalón unitario (señal escalón de amplitud A=1) como señal de prueba en la entrada. La Gráfica 1.3 muestra la respuesta a la entrada escalón unitario, de un sistema representado por la siguiente Función de Transferencia típica de un sistema de primer grado:
\frac{C(s)}{R(s)} = \frac{\boldsymbol1}{\boldsymbol Ts + 1};
La Gráfica 1.3 nos muestra que: “en un sistema de primer grado, el tiempo de asentamiento ts=4T (cuatro veces la Constante de Tiempo T)”.
¿Cuánto vale el tiempo de asentamiento ts para el sistema S1?
Utilizando los resultados anteriores, el tiempo de asentamiento ts para el sistema S1 es:
t_s = 4T = 4 \times 0.137\ \ s
\boldsymbol t_{\boldsymbol s} = 0.548\ \ \boldsymbol sObservación: Como la constante de tiempo no depende de la amplitud de la señal de entrada, el tiempo de asentamiento tampoco depende de dicha amplitud.
¿Cuál es la función de transferencia y la ecuación diferencial del sistema S1?
La siguiente es la Función de Transferencia (FT) de un sistema de primer orden genérico en lazo abierto:
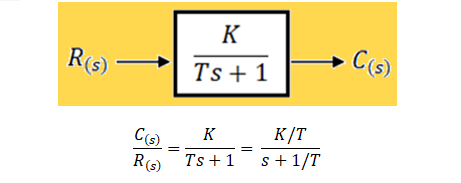
Es decir, que la Función de Transferencia del sistema S1 tiene la siguiente forma:
\frac{Y(s)}{X(s)} = \frac{\boldsymbol K}{\boldsymbol Ts + 1};Ya hemos calculado el valor de la ganancia estática K y la constante de tiempo T del sistema S1, cuya señal de entrada es x(t) y cuya señal de salida es y(t):
Por lo tanto, la Función de Transferencia del sistema S1 es:
\frac{\boldsymbol Y(\boldsymbol s)}{\boldsymbol X(\boldsymbol s)} = \frac{0.46133}{0.137\boldsymbol s + 1}Otra manera de expresar la Función de Transferencia, muy conveniente a la hora de aplicar cálculos algebraicos, es:
Sustituyendo los valores constantes obtenemos que la Función de Transferencia del sistema S1 es:
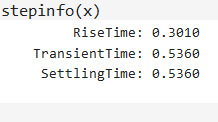
\frac{\boldsymbol Y(\boldsymbol s)}{\boldsymbol X(\boldsymbol s)} = \frac{3.37}{\boldsymbol s + 7.3} ;\ \ \ \ \ (3)Corroboramos este resultado mediante la siguiente simulación en Matlab, Gráfica 1.4:

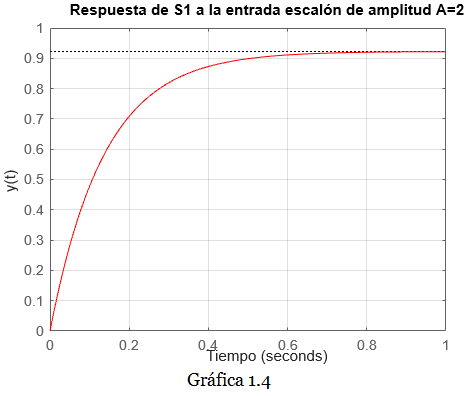
La Gráfica 1.4 presenta la misma forma que la Gráfica 1 del enunciado. El comando damp (como continuación del script anterior) nos permite comprobar el valor de la constante de tiempo T de la curva de la Gráfica 1.4:
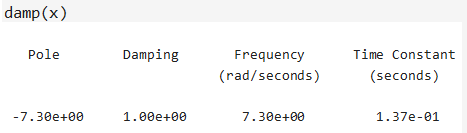
Mientras que el comando stepinfo nos permite comprobar el valor del tiempo de asentamiento ts además de otros parámetros:
Para obtener la Ecuación Diferencial del Sistema (EDS) S1, aplicando simple álgebra primero reordenamos su FT (utilizamos por conveniencia la ecuación 3) de tal manera que obtengamos un polinomio con la variable de salida a la izquierda del lector, y la variable de entrada a la derecha:
Aplicando propiedad asociativa obtenemos el polinomio:
Luego aplicamos la antitransformada utilizando los pares transformados de Laplace más comunes:
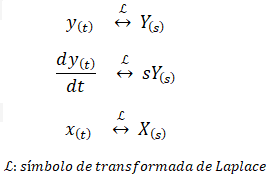
Sustituyendo cada término por su equivalente, el polinomio obtenido anteriormente se transforma en la Ecuación Diferencial del Sistema S1:
\frac{\boldsymbol d\boldsymbol y(\boldsymbol t)}{\boldsymbol d\boldsymbol t} + 7.3 \times \boldsymbol y(\boldsymbol t) = 3.37 \times \boldsymbol x(\boldsymbol t)\ \ \ \ \ \ (4)La ecuación (4) es la Ecuación Diferencial del Sistema S1.
La Ecuación Diferencial del Sistema (EDS) es un modelo dinámico que establece una restricción fundamental sobre ciertas combinaciones de la entrada, la salida y algunas derivadas de ambas señales.
En el modelo del sistema de primer orden, ecuación (4), el mayor orden de las derivadas de la señal de respuesta y(t) debe ser n=1. Sin embargo, el orden de las derivadas sobre la señal de excitación x(t) puede ser cualquier valor igual o mayor a cero. Esto es así porque las operaciones matemáticas definidas sobre la señal de excitación no forman parte del sistema.
¿Cuál es la expresión matemática de y(t), la salida del sistema S1 en el tiempo? ¿Y para una entrada escalón unitario?
Para determinar la expresión matemática de y(t), aplicamos el procedimiento de descomposición en fracciones parciales. Primero despejamos Y(s) de la ecuación (3):
\boldsymbol Y(\boldsymbol s) = \frac{3.37}{\boldsymbol s + 7.3}\boldsymbol X(\boldsymbol s)Recordamos que la entrada al sistema S1 es el escalón de amplitud A=2, es decir:
Al aplicar la transformada de Laplace a x(t) obtenemos:
Sustituimos este resultado en la expresión de Y(s) y descomponemos en fracciones parciales:
Para determinar el valor de las constantes A y B procedemos de la siguiente manera:
Se anulan los determinantes, se aplica asociación y factor común, y obtenemos el siguiente polinomio:
Se igualan los coeficientes de potencia semejantes:
Se sustituye este resultado en la expresión de Y(s):
Utilizamos ahora pares transformados de Laplace comunes:
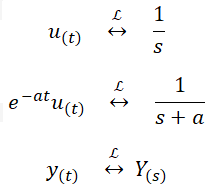
Sustituyendo cada término de la expresión de Y(s) por su equivalente en la tabla anterior, obtenemos la expresión matemática de y(t):
Es decir:
\boldsymbol y(\boldsymbol t) = 0.9226(1 - \boldsymbol e^{- 7.3\boldsymbol t})\boldsymbol u(\boldsymbol t)Observación: como se puede ver, en relación a los parámetros del sistema K y T, la respuesta al escalón de amplitud A tiene la siguiente estructura:
Observación: la salida y(t) es inicialmente cero, y tiende a 0.9226 a medida que el tiempo se hace infinito, tal cual como en la Gráfica 1 del enunciado:
Para la entrada escalón unitario, la entrada es:
Al aplicar la transformada de Laplace a x(t) obtenemos:
Al proceder paso a paso de la misma forma, llegamos a que la expresión matemática de y(t) para una entrada escalón unitario, es:
Observación: la gráfica de la respuesta al escalón unitario tiene la misma forma que la Gráfica 1, la misma constante de tiempo T, pero el valor en estado estable se reduce a la mitad, y la ganancia estática es precisamente ese valor, es decir K=0.4613.
¿Cuál es la velocidad de la respuesta y(t) en t=0 s?
Sabemos de Cálculo que la velocidad es la derivada del desplazamiento, que en este caso viene representado por y(t), la respuesta del sistema de primer orden a la entrada escalón. La derivada a su vez es la pendiente de una recta tangencial a la curva de y(t) en el tiempo t=0 s. Volviendo al modelo estándar de un Sistema de Primer Orden, representado por la siguiente Función de Transferencia con Ganancia Estática K=1, la Gráfica 1.4 muestra la velocidad de respuesta en t=0 s:
\frac{C(s)}{R(s)} = \frac{\boldsymbol1}{\boldsymbol Ts + 1};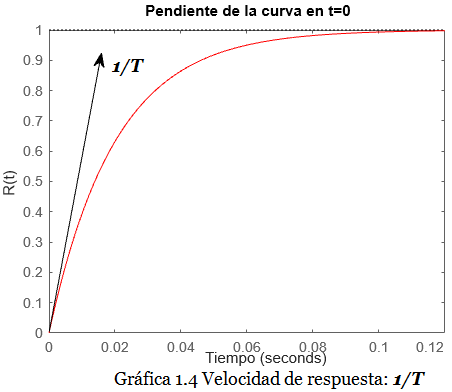
Observación: es necesario reiterar que el resultado anterior sólo es válido cuando la entrada es el escalón unitario.
Cuando la entrada no es el escalón unitario, como en el caso del sistema S1, la velocidad de respuesta en el tiempo t=0 s de la salida y(t) ya no es exactamente 1/T. Para calcularla debemos derivar la expresión matemática obtenida para y(t) en el apartado anterior, y evaluar en t=0 s:
Evaluando en t=0 s:
\frac{\boldsymbol d\boldsymbol y(0)}{\boldsymbol d\boldsymbol t} = 6.735 \times \boldsymbol e^{- 7.3 \times 0} = 6.735En consecuencia, la velocidad de respuesta en el tiempo t=0 s de la salida y(t) es: 6.735 unid/s
Observación:aquí unid se refiere a unidades con las que se mide el desplazamiento.
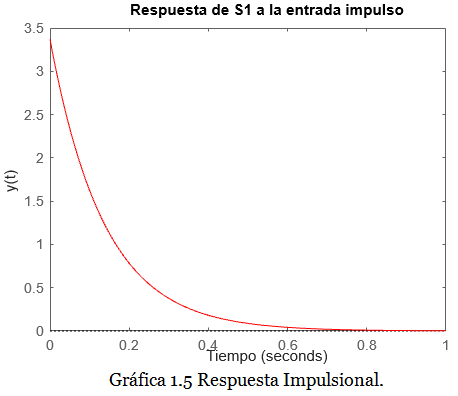
Determinar y Graficar la respuesta impulsional del sistema S1.
Con la Función de Transferencia del sistema S1 expresada por la ecuación (3), podemos determinar la respuesta para cualquier entrada:
En el caso de que la entrada sea un Delta de Dirac δ(t), mejor conocida como entrada impulso, la respuesta del sistema se conoce como respuesta al impulso (o respuesta impulsional). Lo primero por hacer es despejar Y(s) de la ecuación (3) tomando en cuenta la transformada de Laplace de la señal de entrada, que en este caso es 1:
Sustituimos el valor de X(s) en la ecuación (3) y despejamos Y(s):
Es decir, que en el dominio transformado la respuesta al impulso coincide con la función de transferencia del sistema. En realidad, para determinar la respuesta impulsiva, debemos pasar al dominio del tiempo aplicando la anti transformada ayudados con las tablas de pares comunes de transformadas de Laplace:

Si asignamos los siguientes valores a las constantes k y a de la tabla anterior:
Obtenemos la respuesta impulsional del sistema S1:
Observación: como se puede ver, en relación a los parámetros del sistema K y T, la respuesta impulsional tiene la siguiente estructura:
De acuerdo con el resultado anterior, la señal de salida y(t) vale 3.37 en el tiempo t=0 s
Podemos graficar la respuesta impulsional mediante el siguiente script en la consola de Matlab:

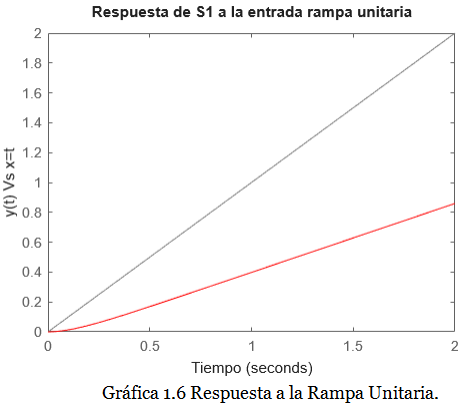
Determinar y Graficar la respuesta a la entrada rampa unitaria del Sistema S1
Utilizando el mismo procedimiento, despejamos Y(s) de la ecuación (3) tomando en cuenta la transformada de Laplace de la señal de entrada en este caso:
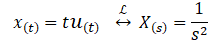
Sustituimos el valor de X(s) en la ecuación (3) y despejamos Y(s):
Aplicamos ahora el método ya utilizado, descomposición en fracciones parciales:
Para determinar el valor de las constantes aplicaremos una técnica alternativa:
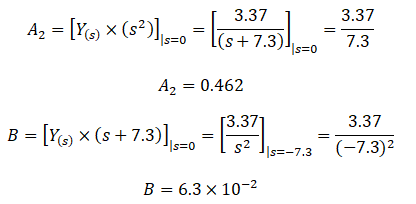
La constante A1 se obtiene derivando respecto a “s” el factor Y(s).s2 y luego evaluando en s=0. Del lado izquierdo de la ecuación (5):
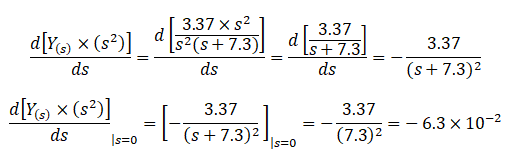
Del lado derecho de la ecuación (5):
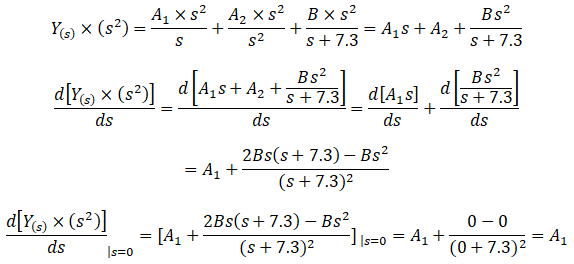
Igualando los resultados obtenidos de ambos lados, concluimos que:
Sustituyendo el valor hallado para cada constante en la ecuación (5) obtenemos:
Ahora aplicamos anti transformada utilizando pares comunes de la tabla de transformadas de Laplace:
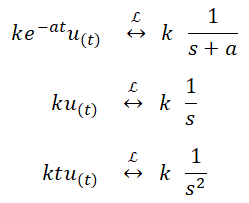
Sustituyendo cada término en la expresión para Y(s) por su equivalente en el tiempo según la tabla anterior, obtenemos que la respuesta a la entrada rampa unitaria del sistema S1 es:
Podemos graficar la respuesta a la entrada rampa unitaria del Sistema S1 mediante el siguiente script en la consola de Matlab:

Misión de Empresa: crear una plataforma académica que contribuya a fortalecer las destrezas y capacidades de futuros ingenieros y emprendedores.
Realizado por: Prof. Larry, Whatsapp: +34747458738.
Email: dademuch@gmail.com
Te puede interesar:
- Se resuelven ejercicios de Sistemas de Primer y Segundo Orden, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…
Te puede interesar:
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs