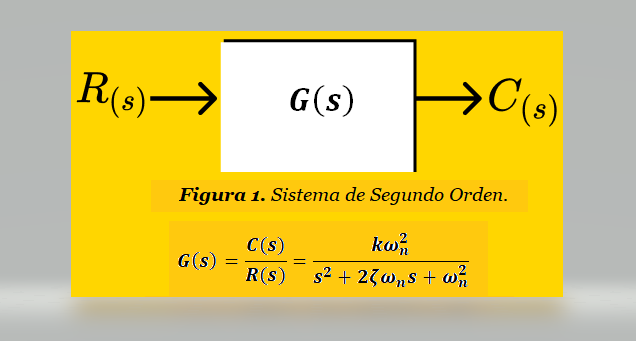
Un Sistema de Segundo Orden se representa generalmente mediante el Diagrama de Bloques y La Función de Transferencia de la Figura 1. La Ganancia Estática k , El Coeficiente de Amortiguamiento ζ y La Frecuencia Natural ωn son los parámetros que definen el comportamiento de un Sistema de Segundo Orden.
¿Qué es un sistema de segundo orden?
Un sistema de segundo orden es aquel cuya relación entrada salida en el dominio del tiempo, está definida por una ecuación diferencial de segundo orden del tipo:
\frac{\boldsymbol d^2\boldsymbol y(\boldsymbol t)}{\boldsymbol d\boldsymbol t^2} + \boldsymbol a_1\frac{\boldsymbol d\boldsymbol y(\boldsymbol t)}{\boldsymbol d\boldsymbol t} + \boldsymbol a_{\boldsymbol o}\boldsymbol y(\boldsymbol t) = \boldsymbol b_{\boldsymbol o}\boldsymbol x(\boldsymbol t);\ para\ cada\ t\ \text{∈}\ \text{R}\ \ (1)La ecuación (1) es la Ecuación Diferencial del Sistema (EDS), un modelo dinámico que establece una restricción fundamental sobre ciertas combinaciones de la entrada, la salida y algunas derivadas de ambas señales.
Aplicando La Transformada de Laplace a la ecuación (1), podemos obtener La Función de Transferencia G(s) del Sistema:
\boldsymbol G(\boldsymbol s) =\frac{\boldsymbol Y(\boldsymbol s)}{\boldsymbol X(\boldsymbol s)}\boldsymbol G(\boldsymbol s) = \frac{\boldsymbol b_0}{\boldsymbol s^2 + \boldsymbol a_1\boldsymbol s + \boldsymbol a_0}En vez de utilizar la ecuación anterior, en ingeniería es conveniente utilizar parámetros que estén relacionados con el comportamiento físico de la respuesta del sistema y con la situación de sus polos en el plano «s». En consecuencia, se utiliza la forma estándar de La Función de Transferencia de un Sistema de Segundo Orden :
\boldsymbol G(\boldsymbol s) = \frac{\boldsymbol K\boldsymbol \omega_{\boldsymbol n}^2}{\boldsymbol s^2 + 2\boldsymbol \zeta \boldsymbol \omega_{\boldsymbol n}\boldsymbol s + \boldsymbol \omega_{\boldsymbol n}^2};\ \ \ (2)\boldsymbol K: Ganancia \ Estática;\ \ \ \ \boldsymbol \omega_{\boldsymbol n}:Frecuencia\ natural\ no\ amortiguada\boldsymbol \zeta: Coeficiente\ de\ Amortiguamiento
El Diagrama de Bloques de la Figura 1 es el modelo gráfico estándar de un sistema de segundo orden a lazo abierto:

La Ganancia Estática K , El Coeficiente de Amortiguamiento ζ y La Frecuencia Natural ωn son los parámetros que definen el comportamiento de un Sistema de Segundo Orden.
La respuesta en el tiempo.
El método más utilizado para estudiar el comportamiento de los sistemas de 2º orden consiste en someter dicho sistema a un conjunto de entradas típicas: el impulso, el escalón unitario, la rampa o una señal sinusoidal.
La simulación de la salida del sistema a la entrada escalón unitario nos permite clasificar los sistemas de segundo orden de la siguiente manera, según la posición de los polos generados en la simulación:
- Subamortiguado (0< ζ <1): polos complejos conjugados con parte real negativa;
- Críticamente amortiguado ( ζ=1 ): polos reales puros, negativos e iguales (polo doble);
- Sobreamortiguado (1<ζ ): polos reales puros, negativos y diferentes;
- Oscilatorio ( ζ=0 ): polos imaginarios puros.
- Inestable ( ζ<0 ): polos complejos conjugados con parte real positiva;
Para repasar la teoría de los Polos y Ceros de un sistema ver: Función de Transferencia – Teoría.
Sistema de segundo orden subamortiguado
De los anteriores, el sistema subamortiguado es de especial importancia para la ingeniería. Como se explicaba anteriormente, el sistema subamortiguado está compuesto por dos polos complejos conjugados con parte real negativa.
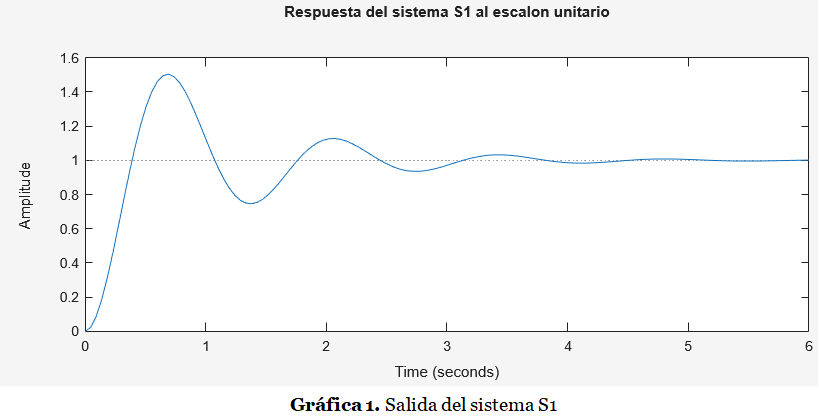
La principal característica de un Sistema de Segundo Orden Amortiguado es que El Coeficiente de Amortiguamiento tiene un valor comprendido entre cero y uno: 0 < ζ < 1 . La forma general de la respuesta transitoria de este tipo de sistemas se ilustra en la Gráfica 1 (Ejercicio S2O-1):
Por cuestiones prácticas que en la solución de los ejercicios se harán evidentes, nos conviene expresar los polos del sistema de segundo orden en términos de dos parámetros nuevos, definidos en función de ζ y ωn : Factor de Atenuación y Frecuencia Amortiguada
\boldsymbol \sigma = \boldsymbol \zeta \boldsymbol \omega_{\boldsymbol n}:\ Factor\ de\ Crecimiento\ ó\ Constante\ de \ Atenuación\boldsymbol \omega_{\boldsymbol d} = \boldsymbol \omega_{\boldsymbol n}\sqrt{1 - \boldsymbol \zeta^2}:\ Frecuencia\ Natural\ AmortiguadaLlamaremos de manera general s1 y s2 a los dos polos complejos conjugados del sistema subamortiguado. En términos de σ y ωd :
\boldsymbol s_1 = - \boldsymbol \sigma + \boldsymbol j\boldsymbol \omega_{\boldsymbol d}\boldsymbol s_2= - \boldsymbol \sigma - \boldsymbol j\boldsymbol \omega_{\boldsymbol d}La ubicación de ambos polos en el plano «s» se observa en la siguiente Figura para el caso del Sistema de Segundo Orden Subamortiguado :
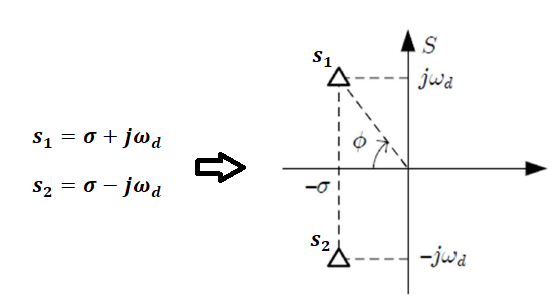
Dónde el ángulo Ø será de gran utilidad a la hora de diseñar sistemas de control y sistemas en general:
\boldsymbol \phi = \mathbf c\mathbf o\mathbf s^{- 1}(\boldsymbol \zeta )La explicación y demostración matemática de las ecuaciones generales para s1 y s2 , así como la práctica para un mayor aprendizaje sobre los parámetros que hemos estudiado hasta ahora se presentan en la SOLUCIÓN Ejercicio S2O-1.
Parámetros más importante de un sistema de 2do. Orden Subamortiguado
La respuesta transitoria de un sistema de segundo orden subamortiguado ante una entrada escalón unitario, ilustrada en la Gráfica 1, por lo general muestra oscilaciones antes de alcanzar el estado estable. En esta etapa de oscilaciones, denominada precisamente respuesta transitoria, los ingenieros han creado un conjunto de parámetros que faciliten el proceso de análisis y diseño de sistemas. Es decir, cuando se requiere o se desea un comportamiento específico de la respuesta transitoria, surgen especificaciones de diseño, las cuáles se dan en término de los siguientes parámetros:
1. Tiempo de estabilización o asentamiento (Settling Time, ts ): el que se requiere para que la curva de respuesta alcance un rango del 2% ó 5% alrededor del valor final, y permanezca en él.
\boldsymbol t_{\boldsymbol s} = \frac{4}{\boldsymbol \sigma }\Rightarrow criterio\ del\ 2\% \boldsymbol t_{\boldsymbol s} = \frac{3}{\boldsymbol \sigma }\Rightarrow criterio\ del\ 5\% Algunos autores prefieren simplemente la siguiente fórmula que se aproxima a las dos anteriores:
\boldsymbol t_{\boldsymbol s} = \frac{\boldsymbol \pi }{\boldsymbol \sigma }2. Tiempo de subida o levantamiento (Rise Time, tr ): el que se requiere para que la curva de respuesta pase del 0 al 90% de su valor final.
\boldsymbol t_{\boldsymbol r} \approx \frac{\boldsymbol \pi - \boldsymbol \theta }{\boldsymbol \omega_d}\Rightarrow \theta = cos^{- 1}(\zeta )3. Tiempo pico (Peak Time, tp ): el que se requiere para que la curva de respuesta alcance el primer pico del sobrepaso o sobreoscilación.
\boldsymbol t_{\boldsymbol p} = \frac{\boldsymbol \pi }{\boldsymbol \omega_d}\Rightarrow \boldsymbol \omega_d = \boldsymbol \omega_n\sqrt{1 - \zeta^2}4. Sobrepaso Máximo o sobreoscilación (Overshoot, Mp ): es el valor pico máximo de la curva de respuesta, medido a partir de la unidad. Si el valor final de la curva de respuesta es diferente de la unidad, se utiliza el porcentaje de sobrepaso máximo
\boldsymbol M_{\boldsymbol p} = \boldsymbol e^{- \frac{\boldsymbol \zeta \boldsymbol \pi }{\sqrt{1 - \boldsymbol \zeta^2}}} =\boldsymbol e^{- \frac{\boldsymbol \pi }{\boldsymbol t_{\boldsymbol g}(\boldsymbol \theta )}}Alternativamente:
\% \boldsymbol M_{\boldsymbol p} = \frac{\boldsymbol y(\boldsymbol t_{\boldsymbol p}) - \boldsymbol y(\infty )}{\boldsymbol y(\infty )}\Rightarrow \boldsymbol y(\boldsymbol t_{\boldsymbol p}):valor\ de\ la\ salida\ en\ tiempo\ pico;\Rightarrow \boldsymbol y(\infty ):valor\ final\ de\ la\ salida
Volviendo a la Gráfica 1, los parámetros antes mencionados se ilustran en la Gráfica 2:
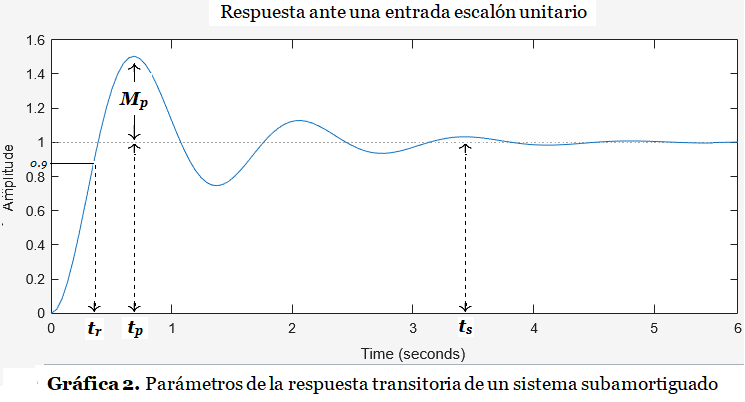
Debido a la importancia del Sistema de Segundo Orden Subamortiguado, los primeros ejercicios a continuación se enfocarán en esta clase de sistemas.
Ejercicios de sistemas de segundo orden
Ejercicio S2O-1: Considere el sistema S1 de segundo orden subamortiguado cuya FT es G(s):
\boldsymbol G(\boldsymbol s) = \frac{22}{\boldsymbol s^2 + 2\boldsymbol s + 22}Realizar los siguientes pasos:
- Determinar la expresión matemática estándar de los polos de un sistema de segundo orden.
- Calcular el valor de La Ganancia Estática K , El Coeficiente de Amortiguamiento ζ y La Frecuencia Natural ωn para el sistema s1.
- En base al paso anterior, ¿Cuáles son los polos del sistema S1? Comprobar en Matlab los resultados anteriores. Graficar la salida de S1 ante una entrada escalón unitario. ¿Se comporta como un sistema subamortiguado?
- Determinar la expresión matemática de la salida en el tiempo de un sistema de segundo orden ante una entrada escalón unitario.
- Calcular el valor de los parámetros más importantes del sistema subamortiguado ante una entrada escalón unitario: tiempo de estabilización, tiempo de subida, tiempo pico, sobreoscilación. Utilizar la simulación del paso anterior para comprobar en Matlab el valor de cada parámetro.
- Determinar la expresión matemática de la salida de un sistema de segundo orden ante una entrada impulso (Respuesta impulsiva).
- Graficar la respuesta impulsiva del sistema S1.
Sistema de Segundo Orden. Parámetros Principales. Ejercicio resuelto para profundizar en la comprensión del análisis teórico de Sistemas.
Encontrarás la solución al ejercicio S2O-1 en el siguiente link: SOLUCIÓN Ejercicio S2O-1.
Procedimiento:
- La respuesta incluye definición teórica de cada concepto y demostración matemática.
- Aplicaremos las técnicas de análisis de libros de texto más utilizados: Ogata, Kuo, Oppenheim, etc.
Ver más ejercicios resueltos en: Sistemas de 2do. Orden – Ejercicios resueltos 1.
Te puede interesar:
- Se resuelven ejercicios de Sistemas de Primer y Segundo Orden, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…
Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos. Al suscribirte podrás contar con excelente material para estudiar y superar con éxito las demandas académicas.
Curso relacionado:
Artículos relacionados:
Función de Transferencia – Teoría y práctica.
Relación entrada-salida del sistema – Teoría y práctica.
Diagrama de Bloques – Teoría y práctica.
Linealidad e Invariancia en el tiempo – Teoría y práctica.
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs
