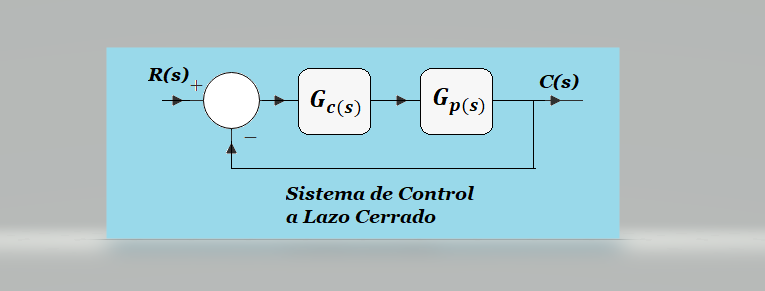
Los Sistemas de Control Automático son aquellos sistemas diseñados para controlar y/o modificar el comportamiento de un sistema dinámico a través de la computación y el proceso denominado realimentación o feedback. La Figura adjunta muestra los componentes básicos de un sistema de control a lazo cerrado: Un controlador cuya función de transferencia (FT) es Gc(s), y una planta con FT Gp(s).
Introducción
Los sistemas de control requieren de la aplicación de algoritmos implementados a través del software de control, muy diferente al software tradicional.
Al alterar el comportamiento de un sistema dinámico, el feedback en un sistema de control busca cumplir los requerimientos que necesita una aplicación específica para funcionar con eficacia: un sistema inestable puede alcanzar un estado estable; un sistema que reacciona demasiado lento ante un estímulo, puede volverse más sensible y rápido; el punto de operación de un sistema electrónico puede mantenerse constante.
A grandes rasgos, se entiende por sistema dinámico aquel en el que los efectos de la acción en su entrada, no se perciben de manera instantánea en la salida, es decir, que el comportamiento del sistema cambia al pasar el tiempo y no de manera instantánea (ejemplos, un dolor de cabeza no desaparece en el mismo instante en que se toma la medicina, la velocidad de un auto no cambia en el mismo instante en que se pisa el acelerador).
Los sistemas dinámicos aparecen en todas las áreas de la ciencia y la tecnología. Es por ello que donde más coincide la Ingeniería de Control con otras disciplinas es en los Modelos de Sistemas, que permiten simular y anticipar el comportamiento de los mismos. Sin embargo, los sistemas de control utilizan modelos con un estilo más enfocado en las entradas y salidas del sistema (input/output modeling) debido a que dichos modelos aportan información relevante sobre los comportamientos del sistema que más interesa controlar, tales como la atenuación de perturbaciones y la interconexión estable entre subsistemas.
Conceptos Básicos
La dinámica de un proceso lineal controlado se ilustra en la Figura 1.
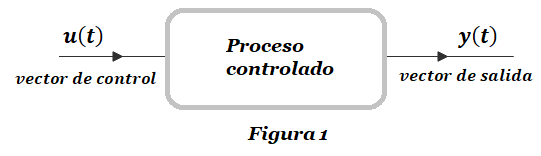
En la Figura 1 la señal de salida y(t) es la variable que se desea controlar (vector de salida), mientras que la señal de entrada u(t) es la señal de control (vector de control). Los sistemas de control se diseñan con el fin de que el vector de salida cumpla con un grupo de especificaciones a su vez diseñadas para que el sistema en su totalidad cumpla con una función o aplicación específica. Por ejemplo, en un sistema de control de posición se busca que la salida «siga» a la señal de entrada que es la señal de referencia de la posición que se desea alcanzar. También un sistema de control puede buscar anular las perturbaciones sobre la variable de salida. Veremos a continuación la distinción entre un Sistema de Control a Lazo Abierto y un Sistema de Control a Lazo Cerrado.
Sistema de Control a lazo abierto
Si la salida no afecta la acción de control se dice que el sistema está en lazo abierto. La Figura 2 ilustra este caso:
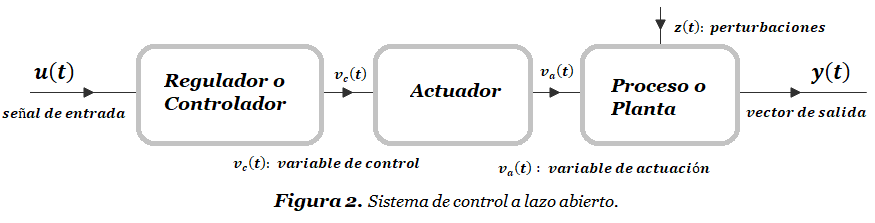
- La señal de entrada u(t) actúa directamente sobre el regulador o controlador. El controlador por tanto no toma en cuenta el valor de la salida y(t) antes de emitir la señal de control vc(t), la cual por medio del actuador genera la variable de actuación va(t) ;
- La variable va(t) actúa sobre la planta y genera el efecto sobre la salida y(t) que la señal de referencia u(t) está intentando producir. Sin embargo, como el sistema no compara la señal de referencia con la salida, el sistema es altamente sensible a las perturbaciones que la señal z(t) pueda generar.
Sistema de Control a lazo cerrado
Si la salida afecta la acción de control se dice que el sistema está en lazo cerrado. Figura 3.
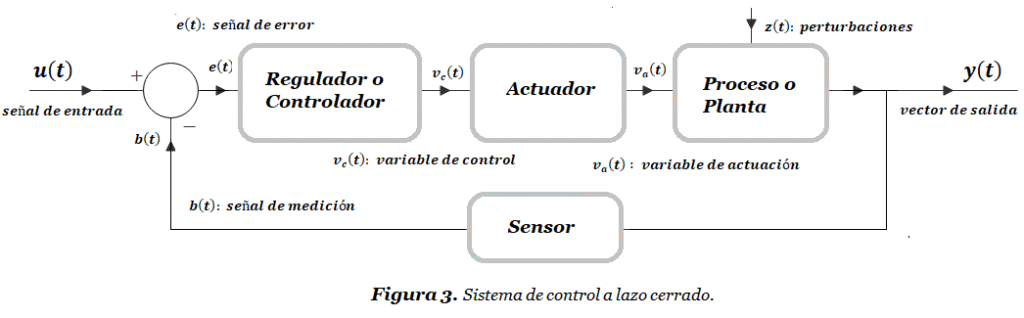
- La señal de entrada u(t) es comparada con la señal de medición b(t) y se genera la señal de error e(t). La señal e(t) actúa sobre el regulador o controlador. El controlador por tanto toma en cuenta el valor de la salida y(t) antes de emitir la señal de control vc(t), la cual por medio del actuador genera la variable de actuación va(t) ;
- La variable va(t) actúa sobre la planta y genera el efecto sobre la salida y(t) que la señal de referencia u(t) está intentando producir. Como el sistema compara la señal de referencia con la salida, el sistema es capaz de responder a las perturbaciones que la señal z(t) pueda generar.
A continuación veremos como se manifiesta cada tipo de control analizado anteriormente, en los modelos básicos de sistemas: sistemas de primer orden y sistemas de segundo orden.
Sistema de primer orden – Control Automático
Un sistema de control a lazo abierto para un sistema de primer orden nos permite aumentar o disminuir la ganancia estática K del sistema, pero no nos permite cambiar su constante de tiempo T, lo que representa una gran limitación para el diseño de un sistema que cumpla con tareas específicas donde, quizás, sea necesario una respuesta más rápida (para un repaso de los parámetros K y T ver Sistema de Primer Orden). En cambio, con un sistema de control a lazo cerrado para un sistema de primer orden, podemos variar ambos parámetros. Vamos a observar esta situación mediante el siguiente ejemplo en el cual se modifica la respuesta de un sistema de primer orden a la entrada escalón unitario. El análisis requiere de una simulación de dicha respuesta.
Sistema de segundo orden – Control Automático
La ganancia estática K de un sistema de segundo orden tiene el mismo significado que para un sistema de primer orden. Surgen en este caso nuevos parámetros: el factor de amortiguamiento relativo ζ será el parámetro más utilizado para estudiar y diseñar la respuesta en el tiempo del sistema de segundo orden, y estará directamente relacionado con su estabilidad ; la frecuencia natural no amortiguada ωn , que viene siendo la frecuencia de oscilación del sistema. Estos dos parámetros permiten a su vez definir otros nuevos para señalar especificaciones de diseño en el caso del sistema subamortiguado (para un repaso ver Sistemas de Segundo Orden).
El Diagrama de Bloques de la Figura 1 es el modelo gráfico estándar de un sistema de segundo orden a lazo abierto:

Controlador PID
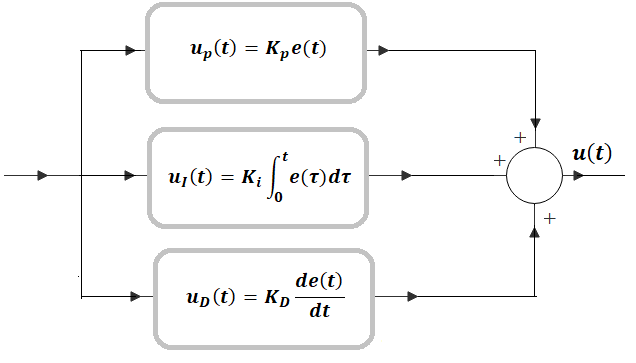
El Controlador PID es un tipo de regulador que aplica una señal de control u(t) a la planta compuesta por una combinación lineal de diferentes señales, tal como lo ilustra la Figura siguiente. Para un análisis detallado ver: Controlador PID.
El diseño del Controlador PID por medio del LGR implica seguir los siguientes pasos : Diseño del PID mediante LGR .
Ejercicios resueltos -Control Automático de Sistemas de Primer Orden
Ejercicio SCA-1: Aplicar un sistema de control a lazo abierto a la planta cuya función de transferencia (FT) es Gp(s) . Utilizar un controlador proporcional con FT Gc(s). Simular en Matlab la respuesta para los siguientes valores de la ganancia del controlador, K =1,2,3 y 4 con el fin de mostrar el cambio en los parámetros k y T de la planta Gp(s). Aplicar luego un sistema de control a lazo cerrado a la planta Gp(s) y simular su respuesta para los mismos valores de K. Mostrar los cambios en los parámetros k y T .
Función\ de\ Transferencia \ de\ la\ planta:\ \ \ \boldsymbol G_{\boldsymbol p}(\boldsymbol s) = \frac{2.9276}{\boldsymbol s + 0.2336}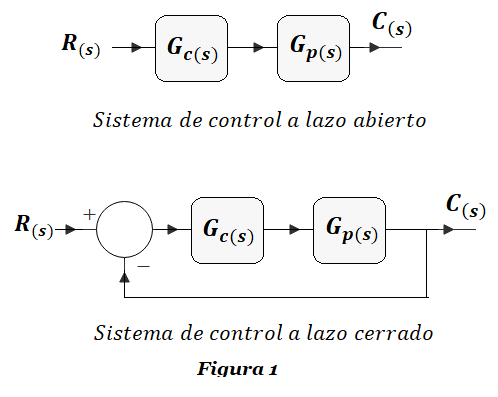
Encontrarás la solución el ejercicio SCA-1 en el siguiente link: SOLUCIÓN Ejercicio SCA-1.
Ejercicios resueltos – Sistemas de Segundo Orden
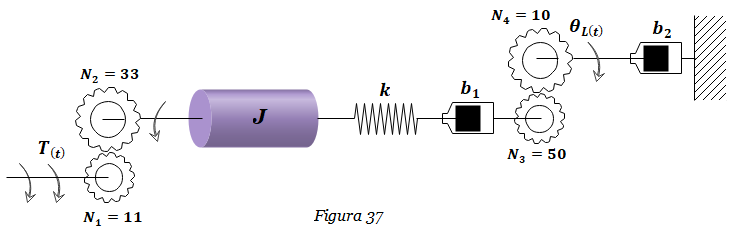
PROBLEMA 1.3: Se pretende controlar un sistema motor-reductor para un brazo robótico cuya función de transferencia G(s) viene definida por:
\boldsymbol G(\boldsymbol s) = \frac{1}{\boldsymbol s^2 + 11\boldsymbol s + 28}- Si se busca un tiempo de asentamiento de 1.25 s y un sobrepaso máximo del 5%, ¿Cuál debería ser la posición de los polos dominantes del sistema en el plano complejo?
- Diseñe el regulador más simple de la familia PID que consiga los requerimientos temporales anteriores y error nulo en estado estacionario. Analice su viabilidad.
Encontrarás la solución al Examen 1-1 en el siguiente link: SOLUCIÓN Examen 1-1
Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos. Al suscribirte podrás contar con excelente material para estudiar y superar con éxito las demandas académicas.
Te puede interesar:
- Se resuelven ejercicios de Sistemas de Sistemas de Control, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…
Curso relacionado:
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs
