Un Sistema de Segundo Orden se representa generalmente mediante el Diagrama de Bloques y La Función de Transferencia de la Figura 1. La Ganancia Estática k , El Coeficiente de Amortiguamiento ζ y La Frecuencia Natural ωn son los parámetros que definen el comportamiento de un Sistema de Segundo Orden.
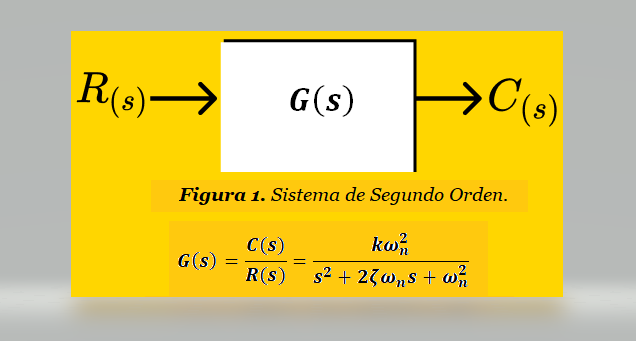
A continuación se resuelve un conjunto de ejercicios de Sistemas de Segundo Orden con el fin de profundizar en el uso y comprensión de los parámetros que caracterizan dichos sistemas.
En esta Guía aprenderás:
- Analizar los polos de un Sistema de Segundo Orden
- Analizar Sistemas Subamortiguados y observar como cambia la salida cuando cambian los parámetros del sistema.
- Analizar los parámetros del sistema con comandos de Matlab.
- Simular en Matlab la respuesta del sistema a las entradas impulso, escalón unitario y rampa,
- Analizar sistemas de primer y segundo orden
- Aplicar álgebra lineal para resolver sistemas de ecuaciones
- Determinar la Función de Transferencia de un sistema a partir de su diagrama eléctrico, de bloques, o mecánico.
- Determinar la Función de Transferencia de un sistema a partir de la Gráfica de su respuesta al escalón unitario.
- Determinar los parámetros de un sistema de segundo orden a partir de diagramas y gráficas del sistema.
Ejercicios resueltos de Sistemas de Segundo Orden
El objetivo en los siguientes ejercicios es realizar un análisis matemático de los Sistemas de Segundo Orden para definir y calcular los parámetros que rigen su comportamiento. Se hace especial enfoque en los sistemas subamortiguados por su importancia para la ingeniería.
Ejercicio S2O-1: Considere el sistema S1 de segundo orden subamortiguado cuya FT es G(s):
\boldsymbol G(\boldsymbol s) = \frac{22}{\boldsymbol s^2 + 2\boldsymbol s + 22}Realizar los siguientes pasos:
- Determinar la expresión matemática estándar de los polos de un sistema de segundo orden.
- Calcular el valor de La Ganancia Estática K , El Coeficiente de Amortiguamiento ζ y La Frecuencia Natural ωn para el sistema s1.
- En base al paso anterior, ¿Cuáles son los polos del sistema S1? Comprobar en Matlab los resultados anteriores. Graficar la salida de S1 ante una entrada escalón unitario. ¿Se comporta como un sistema subamortiguado?
- Determinar la expresión matemática de la salida en el tiempo de un sistema de segundo orden ante una entrada escalón unitario.
- Calcular el valor de los parámetros más importantes del sistema subamortiguado ante una entrada escalón unitario: tiempo de estabilización, tiempo de subida, tiempo pico, sobreoscilación. Utilizar la simulación del paso anterior para comprobar en Matlab el valor de cada parámetro.
- Determinar la expresión matemática de la salida de un sistema de segundo orden ante una entrada impulso (Respuesta impulsiva).
- Graficar la respuesta impulsiva del sistema S1.
Encontrarás la solución al ejercicio S2O-1 en el siguiente link: SOLUCIÓN Ejercicio S2O-1.
PROBLEMA 1.1: Calcula la expresión de la salida v0(t) en función del tiempo para el circuito RLC de la Figura 1, ante una entrada vi(t)=u0(t) (escalón unitario) con R=2 Ω, L=1 H y C=1/5 F. Considere las condiciones iniciales iguales a cero.
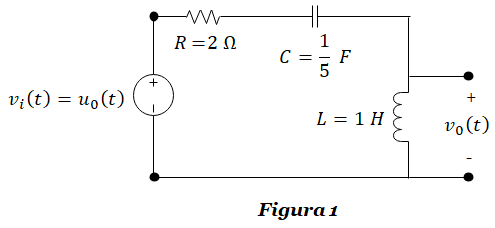
Encontrarás la solución al Problema 1-1 en el siguiente link: SOLUCIÓN Examen 1-1.
PROBLEMA 1.2: Diseña el sistema de control de la Figura 2, determinando el valor de las constantes A, B y C (suponga una acción proporcional de control) para que la forma de la curva de la respuesta y(t) a una entrada x(t) escalón unitario sea la que muestra la Gráfica 1.
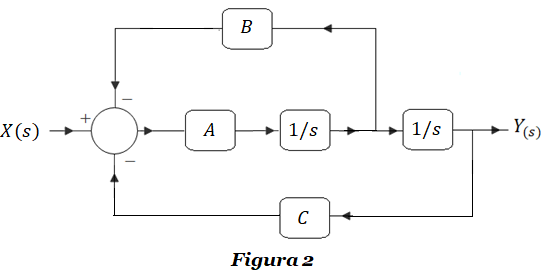
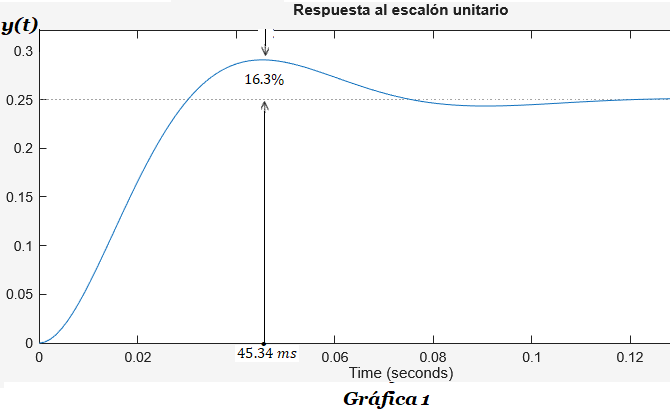
Encontrarás la solución al Problema 1-2 en el siguiente link: SOLUCIÓN Examen 1-1.
PROBLEMA 1.3: Dada la función de transferencia directa G(s) para un sistema de control con realimentación unitaria. Se pretende controlar un sistema motor-reductor para un brazo robótico:
\boldsymbol G(\boldsymbol s) = \frac{1}{\boldsymbol s^2 + 3\boldsymbol s + 2}- Si se busca un tiempo de asentamiento de 0.9 s y un sobrepaso máximo del 5%, ¿Cuál debería ser la posición de los polos dominantes del sistema en el plano complejo?
- Diseñe el regulador PID que consiga cumplir con los requerimientos temporales anteriores.
Encontrarás la solución al Problema 1-3 en el siguiente link: SOLUCIÓN Examen 1-1.
Te puede interesar:
- Se resuelven ejercicios de Determinar la Función de Transferencia, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…
Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos. Al suscribirte podrás contar con excelente material para estudiar y superar con éxito las demandas académicas.
Curso relacionado:
Artículos relacionados:
- Función de Transferencia – Teoría.
- Sistemas de Primer Orden – Teoría.
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs
