Transformación de la variable independiente – Examen resuelto SS1-1 (Señales y Sistemas) -

Transformación de la variable independiente en señales y sistemas.

Ejercicio SS1-1.

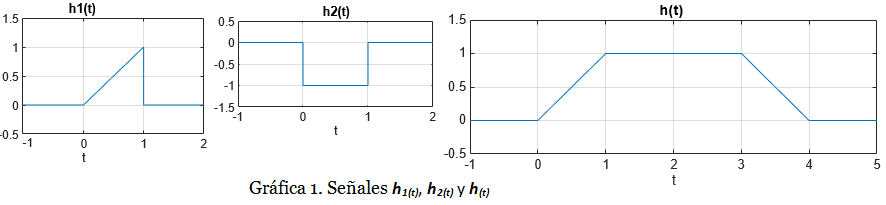
Considere 3 señales denominadas h_1(t), h_2(t) y h_(t). La Gráfica 1 muestra las tres señales.

Responda las siguientes preguntas:

Escriba la expresión de h_(t) utilizando las señales h_1(t) y h_2(t). Debe emplear transformaciones de la variable independiente necesarias.
¿Es h_(t) una señal definida en potencia media o en energía? Justifique su respuesta y calcule cada una.
Graficar dh(t)/dt. Obtenga su expresión analítica utilizando señales elementales.
La señal z_(t) se define como z_(t)=-h_(-2t+6). Graficar z_(t).

Expresión de h_(t) utilizando las señales h_1(t) y h_2(t).

La estrategia que proponemos es considerar que la señal h_(t) presenta tres regiones claramente definidas. En la primera región h_(t) es una línea recta de pendiente positiva. En la segunda región h_(t) es una constante. En la tercera región h_(t) es una línea recta de pendiente positiva.

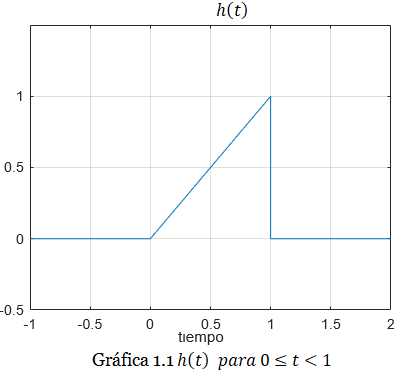
Región 1 (0≤ t <1): la gráfica de h_(t) tiene la misma forma que h_1(t). Por lo tanto:

\boldsymbol h(\boldsymbol t) = \boldsymbol h_1(\boldsymbol t)\boldsymbol \ \ p\boldsymbol a\boldsymbol r\boldsymbol a \ \ 0 \leq \boldsymbol t < 1

Esto lo podemos observar en la Gráfica 1.1:

Región 2 (1≤ t <3): la gráfica de h_(t) es una constante, por lo tanto debemos utilizar la gráfica de h_2(t) y luego de aplicar las siguientes transformaciones transformaciones a la variable independiente:

h (t) = - h_{2} (t)

: inversión de amplitud

h (t) = - h_{2} (t - 1)

: desplazamiento temporal

h (t) = - h_{2} (t - 2)

: desplazamiento temporal

Las tres transformaciones las podemos ver en la Gráfica 1.2:

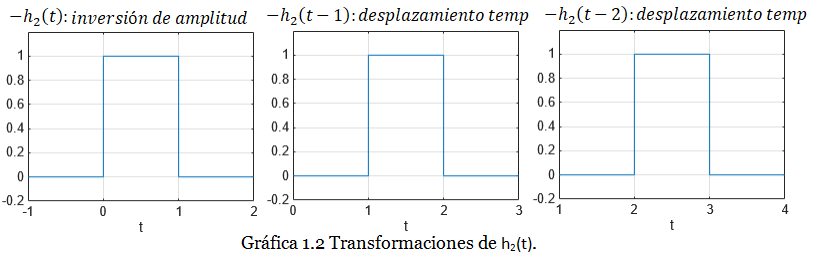
En conclusión:

h (t) = - h_{2} (t - 1) - h_{2} (t - 2) p a r a 1 \leq t < 3

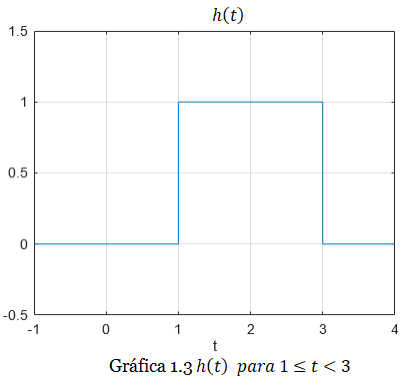
Este resultado lo podemos observar en la Gráfica 1.3:

Alternativamente tenemos otra vía y podemos aplicar este grupo de transformaciones sobre h_2(t):

h (t) = - h_{2} (t)

: inversión de amplitud

h (t) = - h_{2} (\frac{t}{2})

: expansión temporal

h (t) = - h_{2} (\frac{t - 1}{2})

: deplazamiento temporal

Las tres transformaciones las podemos ver en la Gráfica 1.4:

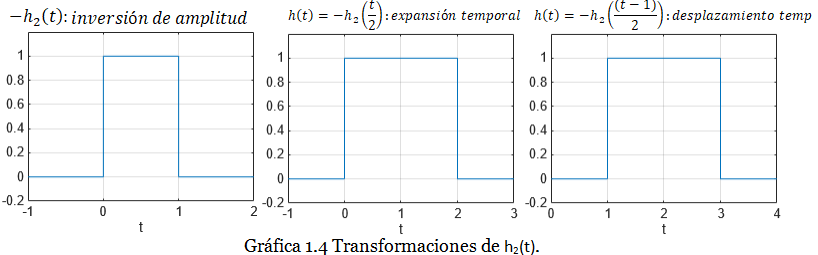
En conclusión:

h (t) = - h_{2} (0.5 (t - 1)) p a r a 1 \leq t < 3

Cómo se puede ver este último resultado resulta una fórmula más compacta.

Región 3 (3≤ t <4): la gráfica de h_(t) es una recta con pendiente negativa. Deberíamos utilizar la gráfica de h_1(t) y luego de aplicar las siguientes transformaciones a la variable independiente:

h (t) = h_{1} (- t)

: reflexión o inversión

h (t) = h_{1} (- t + 4)

: desplazamiento temporal

Las dos transformaciones las podemos ver en la Gráfica 1.5:

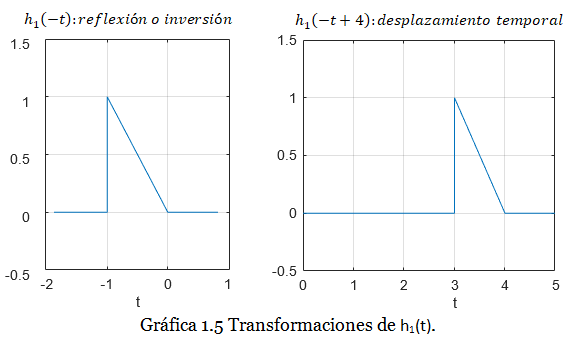
En conclusión:

h (t) = h_{1} (- t + 4) p a r a 3 \leq t \leq 4

En definitiva, se suman las tres regiones y obtenemos:

h (t) = h_{1} (t) - h_{2} (0.5 (t - 1)) + h_{1} (- t + 4) p a r a t o d o t

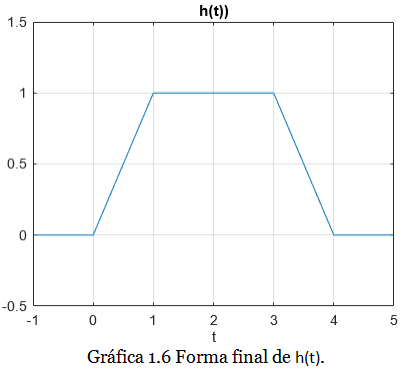
Observamos el resultado final de combinar las tres regiones, en la Gráfica 1.6:

¿Es h_(t) una señal definida en potencia media o en energía?

Para decidir si la seña h(t) está definida en potencia media o en energía, revisamos a continuación los siguientes criterios.

Criterios para señales de energía y de potencia.

1. Una señal x es de potencia si y solo si su contenido de potencia promedio P es finita y mayor que cero (0 <P_x< ∞), lo cual implica que su contenido de energía es infinita (E_x → ∞). Es el caso de las señales periódicas:

o < P_{M} < \infty; E \to \infty

: Señal definida en potencia media (vatios)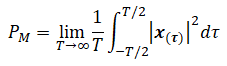

2. Una señal x es de energía si y solo si su contenido de energía E es finita (E_x< ∞), lo cual implica que su contenido de potencia es cero (P_x= 0). Es el caso de las señales que tienen un inicio y un final (señales de duración limitada):

E < \infty; P_{M} = 0

: Señal definida en energía (joules)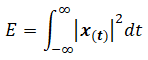

3. Una señal x que no satisface ninguna de las condiciones anteriores entonces no es una señal de potencia o de energía. Ejemplo, la función rampa.

4. Si se trata de una señal sinusoidal de amplitud A se puede demostrar que la potencia promedio es directamente:

P_{M} = \frac{A^{2}}{2}

5. Se define potencia promedio como la potencia en un intervalo de tiempo:

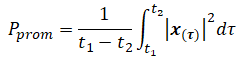
Con estos criterios pasamos ahora a evaluar si la señal h_(t) que nos interesa es una señal de energía o de potencia promedio.

Debido a que h_(t) es una señal de duración limitada (ver Gráfica 1.6), ella es claramente una señal definida en energía. Calculamos esta energía de la siguiente manera:

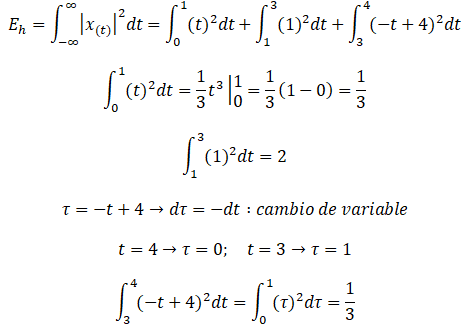
Por lo tanto:

E_{h} = 2 (\frac{1}{3}) + 2 = \frac{8}{3} j o u l e s

Por su parte, la potencia media es:

P_{M h} = 0 v a t i o s

Graficar dh(t)/dt. Obtenga su expresión analítica utilizando señales elementales

Aprovechamos que la señal h_(t) presenta tres regiones claramente definidas. En la primera región h_(t) es una línea recta de pendiente positiva, por lo tanto la derivada de h_(t) en esta región da como resultado una constante de igual valor que la pendiente de la recta. En la segunda región h_(t) es una constante, por lo tanto la derivada de h_(t) en esta región es cero. En la tercera región h_(t) es una línea recta de pendiente positiva, por lo tanto la derivada de h_(t) aquí da como resultado una constante de valor negativo. El resultado se observa en la Gráfica 1.7:

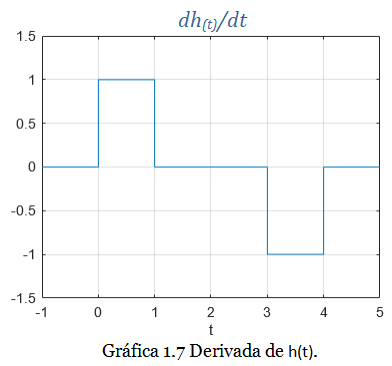
Observación: en algunas ocasiones será necesario determinar primero la expresión matemática de la señal para luego derivar. En este caso hemos dicho que h_(t) presenta tres regiones. En cada región la expresión matemática de la derivada de h_(t) es:

Región 1::

h (t) = t \to \frac{d h (t)}{d t} = 1 p a r a 0 \leq t < 1

Región 2::

h (t) = 1 \to \frac{d h (t)}{d t} = 0 p a r a 1 \leq t < 3

Región 3::

h (t) = - t + 4 \to \frac{d h (t)}{d t} = - 1 p a r a 3 \leq t < 4

Para expresar dh_(t)/dt con funciones básicas, definimos la señal elemental “pulso rectangular ” de la siguiente manera:

Definición: La señal pulso rectangular (o pulso cuadrado) es aquella señal analógica cuya amplitud es uno (1) para un cierto intervalo finito de valores de la variable independiente y cero (0) en el resto:

Algunos centros académicos prefieren la siguiente notación para la señal pulso rectangular:

r e c t (\frac{t - t_{0}}{T})

Utilizando esta última notación, podemos expresar dh_(t)/dt de la siguiente manera:

\frac{d h (t)}{d t} = r e c t (\frac{t - \frac{1}{2}}{1}) - r e c t (\frac{t - \frac{7}{2}}{1})

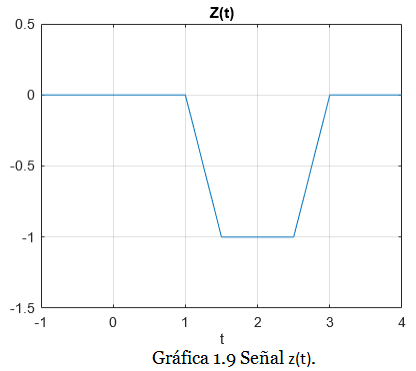
Graficar z_(t).

La señal z_(t) se define como:

z (t) = - h (- 2 t + 6)

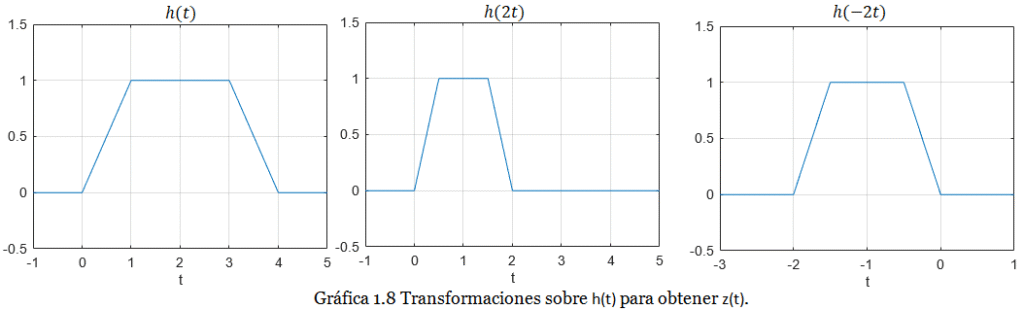
El primer paso consiste en reescribir la transformación de la variable independiente:

z (t) = - h (- 2 (t - 3))

El orden en que se producen las transformaciones de la variable independiente el siguiente: compresión por un factor de 2:

h (2 t)

Luego inversión temporal:

h (2 (- t)) = h (- 2 t)

Luego desplazamiento a la derecha (retraso):

h (2 (- t)) = h (- 2 (t - 3))

Y por último inversión de amplitud:

- h (2 (- t)) = h (- 2 (t - 3))

A continuación la Gráfica 1.8 muestra cada paso:

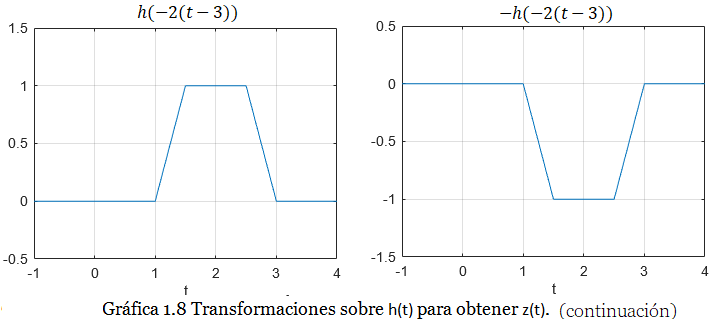
Es evidente que la gráfica definitiva para la señal z_(t) es la Gráfica 1.9:

Te puede interesar:

Se resuelven ejercicios de Señales y Sistemas 1 y 2, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
Clases Online: Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…

Ejercicio SS1-1.

Expresión de h(t) utilizando las señales h1(t) y h2(t).

¿Es h(t) una señal definida en potencia media o en energía?

Criterios para señales de energía y de potencia.

Graficar dh(t)/dt. Obtenga su expresión analítica utilizando señales elementales

Graficar z(t).

Related Posts

Expresión de h_(t) utilizando las señales h_1(t) y h_2(t).

¿Es h_(t) una señal definida en potencia media o en energía?

Graficar z_(t).