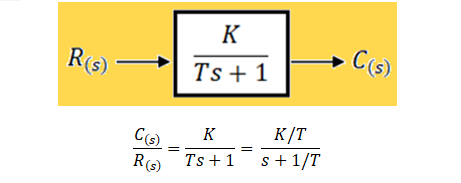
A continuación se ejecutan los pasos para el Diseño de un Controlador PD. El objetivo principal es utilizar El Lugar Geométrico de las Raíces (LGR) y la simulación en Matlab para obtener el resultado más aceptable posible usando además la teoría clásica sobre Sistemas de Segundo Orden Amortiguado. Este ejemplo es además el Problema 1.3 de nuestro primer examen de Sistemas de Control.
PROBLEMA 1.3: Dada la función de transferencia directa G(s) para un sistema de control con realimentación unitaria. Se pretende controlar un sistema motor-reductor para un brazo robótico:
\boldsymbol G(\boldsymbol s) = \frac{1}{\boldsymbol s^2 + 3\boldsymbol s + 2}- Si se busca un tiempo de asentamiento de 0.9 s y un sobrepaso máximo del 5%, ¿Cuál debería ser la posición de los polos dominantes del sistema en el plano complejo?
- Diseñe el regulador PD que consiga cumplir con los requerimientos temporales anteriores.
Respuesta 1.3
1er. Paso: Aplicamos la teoría aprendida en Sistemas de Segundo Orden para calcular los polos dominantes o polos deseados según las especificaciones de diseño dadas en términos del tiempo de asentamiento y el sobrepaso máximo:
Ya habíamos descrito en teoría que los polos para un sistema de segundo orden subamortiguado son complejos conjugados cuya forma es la siguiente:
\boldsymbol s_{1,2} = - \boldsymbol \sigma \pm\boldsymbol j\boldsymbol \omega_{\boldsymbol d}Dónde:
\boldsymbol \sigma = \boldsymbol \zeta \boldsymbol \omega_{\boldsymbol n\boldsymbol ;}\ \ \ \ \boldsymbol \omega_{\boldsymbol d} = \mathbf \omega_{\mathbf n}\sqrt{1 - \boldsymbol \zeta^2}De los datos que aporta el enunciado (tiempo de asentamiento ts y sobrepaso máximo Mp) obtenemos el valor de σ mediante el siguiente procedimiento:
t_s = \frac{\pi }{\sigma }\Rightarrow \sigma = \frac{\pi }{t_s} = \frac{\pi }{0.9\ s}\Rightarrow \boldsymbol \sigma = 3.49\ rad/ sLuego, obtenemos el valor de ζ utilizando el Mp :
\boldsymbol M_{\boldsymbol p} = \boldsymbol e^{- \frac{\boldsymbol \pi }{\boldsymbol t_{\boldsymbol g}(\boldsymbol \theta )}}\Rightarrow \sigma = \ln (M_p) = - \frac{\pi }{t_g\theta }\Rightarrow t_g\theta = - \frac{\pi }{\ln (M_p)} t_g\theta = - \frac{\pi }{\ln (0.05)} = 1.048\Rightarrow \theta = t_g^{- 1}(1.048) = 46.36\degree \zeta = cos(46.36\degree )\Rightarrow \boldsymbol \zeta = 0.69
Teniendo σ y ζ podemos obtener ωn mediante:
\omega_n = \frac{\sigma }{\zeta } = \frac{3.49}{0.69}\Rightarrow \boldsymbol \omega_{\boldsymbol n} = 5.06Con estos datos obtenemos ωd :
\omega_d = \omega_n\sqrt{1 - \zeta^2} = (5.06)\sqrt{1 - (0.69)^2\Rightarrow }\boldsymbol \omega_{\boldsymbol d} = 6.44En conclusión, los polos dominantes deseados (Pds) para un sistema de segundo orden subamortiguado que cumpla con tiempo de asentamiento ts y sobrepaso máximo Mp del enunciado, son:
\boldsymbol s_1 = - 3.49 + \boldsymbol j3.66
\boldsymbol s_2 = - 3.49 - \boldsymbol j3.66
2do. Paso: Para diseñar el regulador PID, aplicaremos el algoritmo presentado en Diseño del PID mediante LGR :
Paso 2.1: Dibujar el LGR y localizar los Pds . En base a los requerimientos de diseño dados en términos del tiempo de asentamiento y el sobrepaso máximo, ya hemos calculado en el paso anterior los Pds :
\boldsymbol s_1 = - 3.49 + \boldsymbol j3.66
\boldsymbol s_2 = - 3.49 - \boldsymbol j3.66
El sistema a controlar es un sistema de segundo orden un Tipo 0:
\boldsymbol G(\boldsymbol s) = \frac{1}{\boldsymbol s^2 + 3\boldsymbol s + 2}La función G(s) tiene dos polos en s= – 1 y s= – 2:
G(s) = \frac{1}{\left(s + 1\right)\left(s + 2\right)}G(s) es la Función de Transferencia Directa de un sistema de control a lazo cerrado con realimentación unitaria como el de la Figura 1:
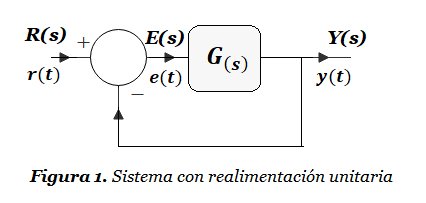
La Figura 1 representa el sistema de control antes de añadir el controlador PID (antes de la compensación). Para dibujar el LGR necesitamos conocer G(s)H(s), la Función de Transferencia del sistema de control a lazo abierto. En este caso, como la realimentación es unitaria , obtenemos que G(s)H(s)=G(s).
Para dibujar el LGR manualmente ver El Lugar Geométrico de las Raíces . Por economía de espacio utilizaremos el siguiente código en la consola de Matlab:
>> G=tf([1],[1 3 2]);
>> rlocus(G)
>> title('LGR ejer1.3 exa1 antes de la compensación')El LGR lo podemos ver en la Figura 2. Es evidente que los polos deseados s1 y s2 no pertenecen al LGR del sistema de control de la Figura 1.
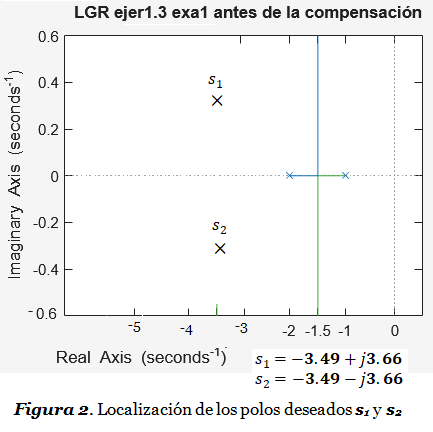
Paso 2.2: Incorporamos Acción Necesaria: Proporcional-Derivativa. El LGR de la Figura 2 nos demuestra que los polos deseados s1 y s2 no pertenecen al LGR. Debemos cumplir con los requerimientos de respuesta transitoria, por lo que es necesaria la acción derivativa para obligar al LGR a incluir los polos deseados. De acuerdo con Controlador PID, para aplicar la acción proporcional-derivativa (PD), el controlador deberá tener la siguiente función de transferencia:
Controlador\ PD:G_c(s) = K(s + a)
La acción derivativa del controlador PID añade un cero en s = – a . La Figura 3 muestra como añadir el controlador PD al sistema de la Figura 1:
Añadimos este controlador al sistema de la Figura 1:
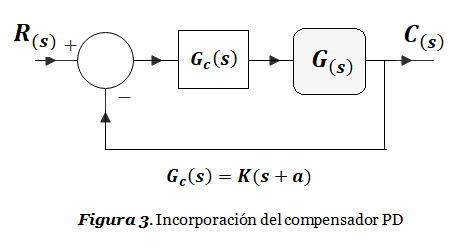
Debemos ajustar la constante a mediante el criterio del argumento, hasta que el LGR pase por los Polos dominantes. Ajustar luego K mediante el criterio del módulo.
En la Figura 4 aparecen los factores para aplicar el criterio del argumento (para repasar este tema ver El Lugar Geométrico de las Raíces ):
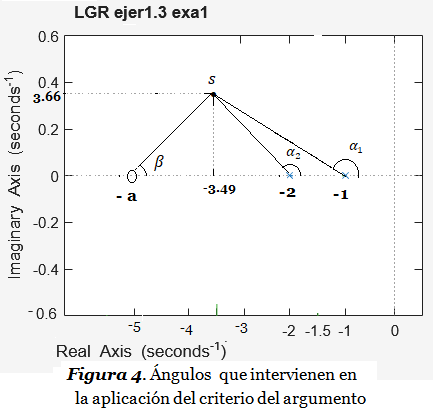
Paso 2.3: Calcular el valor de la constante «a» aplicando el criterio del argumento. En la Figura 4 observamos el punto de prueba “s” cercano al polo dominante deseado s1:
s = - 3.49 + j3.66
Los polos ubicado en s = – 1 y s = – 2 pertenecen al LGR del sistema. Es importante notar que la función de transferencia a lazo abierto cambia (ahora es el producto Gc(s)G(s)) .
Calcularemos el valor de a mediante El Criterio del Ángulo:
\angle G_c(s)G(s) = \pm 180\degree \ldotp (2q + 1);\ \ \ \ q = 0,1,2.\ldotp \ldotp
De todas las opciones posibles que nos ofrece la ecuación anterior seleccionamos la que más nos convenga:
\angle G_c(s)G(s) = \sum polos - \sum ceros = 180\degree \Rightarrow
Tomando en cuenta las notaciones asignadas a los ángulos de la Figura 4:
\Rightarrow (\alpha_1 + \alpha_2) - \beta = 180\degree
Utilizando la Figura 4 obtenemos el valor de cada ángulo (Los ángulos de las variables complejas sobre el LGR y que inician en los polos y ceros en lazo abierto, se miden en sentido contrario a las manecillas del reloj):
\alpha_1 = 180\degree - t_g^{- 1}\left(\frac{3.66}{3.49 - 1}\right) = 180\degree - 55.77\degree\Rightarrow \boldsymbol \alpha_1 = 124\ldotp 23\degree \alpha_2 = 180\degree - t_g^{- 1}\left(\frac{3.66}{3.49 - 2}\right) = 180\degree - 67.85\degree \Rightarrow \boldsymbol \alpha_2 = 112\ldotp 15\degreeEn consecuencia:
\Rightarrow \beta = 124.23\degree + 112.15\degree - 180\degree = 56\ldotp 38\degree
t_g\left(\beta \right) = t_g\left(56.38\degree \right) = 1.50
t_g\left(\beta \right) = \frac{3.66}{\boldsymbol a - 3.49} = 1.50\Rightarrow \boldsymbol a = 5.92Conociendo el valor de «a» sabemos que el controlador PD tiene la siguiente FT:
Controlador\ PD:G_c(s) = K(s + 5.92)
Es decir, la Función de Transferencia a lazo abierto es:
G_c(s) G(s)= K\frac{(s + 5.92)}{(s + 1)(s + 2)}La Función de Transferencia a lazo abierto nos permite dibujar el LGR del sistema de control después de la compensación:
>> G=tf([1],[1 3 2]);
>> Gc=tf([1 5.92],[1]);
>> K=1;
>> GH=K.*Gc*G;
>> rlocus(GH)
>> title('LGR ejer1.3 exa1 después de la compensación PD')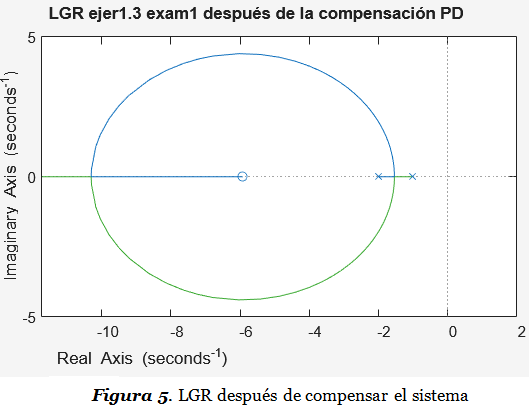
Un zoom nos permite comprobar que los Pds ahora pertenecen al LGR, y que en esos puntos se cumple el sobrepaso solicitado (overshoot 4.98%):
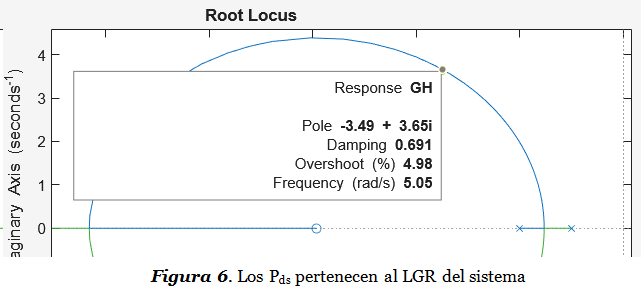
Paso 2.4: Ajustar el valor de la constante K aplicando el Criterio del Módulo. Ajustar K es colocar el sistema en el punto adecuado del LGR tal que las raíces del sistema a lazo cerrado estén localizadas en el punto resaltado en la Figura 6. El siguiente script de Matlab nos permite ver cuáles son las raíces del polinomio característico (los polos del sistema a lazo cerrado) cuando K=1.
>> G=tf([1],[1 3 2]);
>> Gc=tf([1 5.92],[1]);
>> K=1;
>> GH=K.*Gc*G;
>> sys=feedback(GH,1);
>> damp(sys)
Pole Damping Frequency
(rad/seconds)
-2.00e+00 + 1.98e+00i 7.11e-01 2.81e+00
-2.00e+00 - 1.98e+00i 7.11e-01 2.81e+00 De acuerdo con el resultado anterior, cuando K=1 los polos del sistema a lazo cerrado son s1= – 2 +j1.98 y s2= – 2 -j1.9 .
Para que las raíces del polinomio característico coincidan con los Pds , vamos a ajustar la Ganancia K mediante el Criterio del Módulo. Para esto se consideran los módulos de las distancias entre cada cero y cada polo al punto de prueba “s”, tal como lo representa la Figura 7:
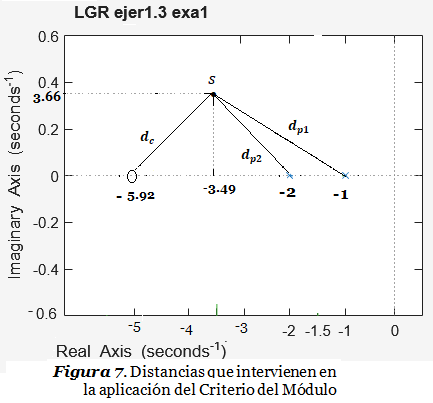
El Criterio del Módulo expresa que:
\boldsymbol G_{\boldsymbol c}(\boldsymbol s)\boldsymbol G(\boldsymbol s) = - \frac{1}{\boldsymbol K}
De dónde obtenemos que:
K = \frac{1}{\left|G_c\left(s\right)G\left(s\right)\right|} = \frac{\left|s + 1\right| \times \left|s + 2\right|}{\left|s + 5.92\right|} = \frac{d_{p1} \times d_{p2}}{d_c}\Rightarrow K = \frac{\sqrt{\left(3.49 - 1\right)^2 + \left(3.66\right)^2} \times \sqrt{\left(3.49 - 2\right)^2 + \left(3.66\right)^2}}{\sqrt{\left(5.92 - 3.49\right)^2 + \left(3.66\right)^2}}\Rightarrow \boldsymbol K = 3.9831En el siguiente script vemos cuáles son los polos del sistema a lazo cerrado cuando K=3.9831 :
>> G=tf([1],[1 3 2]);
Gc=tf([1 5.92],[1]);
>> K=3.9831;
>> GH=K.*Gc*G
GH =
3.983 s + 23.58
---------------
s^2 + 3 s + 2
>> sys=feedback(GH,1);
>> damp(sys)
Pole Damping Frequency
(rad/seconds)
-3.49e+00 + 3.66e+00i 6.90e-01 5.06e+00
-3.49e+00 - 3.66e+00i 6.90e-01 5.06e+00 El resultado anterior muestra que seleccionando la Ganancia K=3.9831 los polos del sistema a lazo cerrado son s1= – 3.49 +j3.66 y s2= – 3.49 -j3.66 , que son los polos dominantes deseados. Utilizando el script anterior podemo averiguar el valor del tiempo de asentamiento (settling Time 1.02 s). No es exactamente lo que se solicitaba pero resulta una aproximación aceptable.
>> stepinfo(sys)
RiseTime: 0.2698
SettlingTime: 1.0201
En conclusión, el regulador PID necesario para cumplir con los requerimientos temporales de diseño, tiene la siguiente Función de Transferencia:
G_c = 3.9831(\mathbf s + 5.92)
La siguiente simulación muestra la respuesta del sistema de control a la entrada escalón unitario, antes y después de la compensación PD:
>> sys2=feedback(G,1);
>> step(sys,sys2) 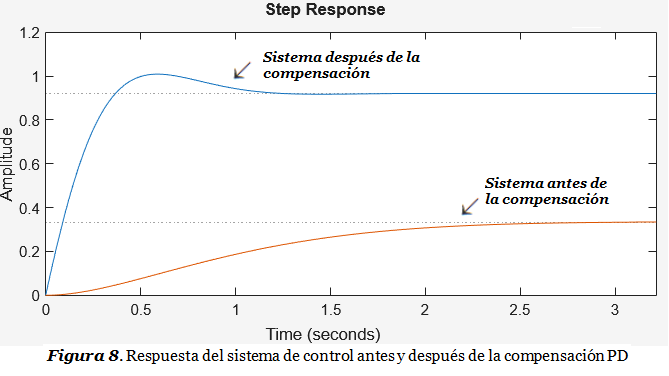
Te puede interesar:
- Se resuelven ejercicios de Determinar la Función de Transferencia, Sistemas de Control, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…
Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos. Al suscribirte podrás contar con excelente material para estudiar y superar con éxito las demandas académicas.
Curso relacionado:
Artículos relacionados:
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs