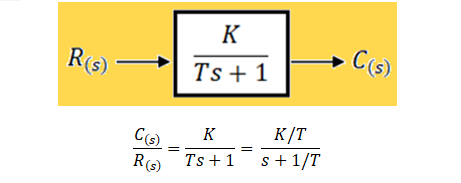
Para entender el concepto de Función de Transferencia a lazo abierto, o Función de Transferencia a lazo cerrado, utilizamos el diagrama de bloques de la Figura 1:
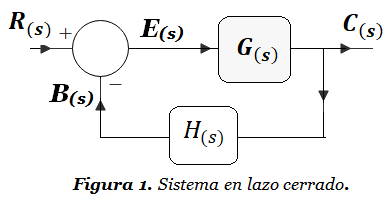
En la Figura 1 G(s) es la función de transferencia de la planta y H(s) es la función de transferencia del sensor. El sensor genera una señal B(s) que se realimenta al punto de suma, donde se compara con la señal de referencia R(s), generando una señal denominada señal de error E(s) . Aplicando álgebra de bloques a la Figura 1 podemos ver claramente que la señal de salida C(s) se puede obtener multiplicando E(s) por G(s) :
C(s) = G(s)E(s)
Es decir:
G(s) = \frac{C(s)}{E(s)}\ \ \ \ (1)A la función G(s) de la ecuación (1) se le conoce como Función de transferencia de trayectoria directa (cociente entre la salida y la señal de error) considerando el sistema de la Figura 1:
Función de Transferencia Directa: cociente entre la señal de salida C(s) y la señal de error E(s) :
\boldsymbol G(\boldsymbol s) = \frac{\boldsymbol E(\boldsymbol s)}{\boldsymbol C(\boldsymbol s)}Utilizando las ecuaciones anteriores podemos calcular la señal de realimentación B(s) :
B(s) = C(s)H(s) = E(s)G(s)H(s)
Es decir:
G(s)H(s) = \frac{B(S)}{E(s)}\ \ \ \ (2)Al producto G(s) H(s) de la ecuación (2) se le conoce como Función de transferencia en lazo abierto (cociente entre la señal de realimentación y la señal de error)
Función de Transferencia en Lazo Abierto: cociente entre la señal de realimentación B(s) y la señal de error E(s) :
\boldsymbol G\left(\boldsymbol s\right)\boldsymbol H\left(\boldsymbol s\right) = \frac{\boldsymbol B(\boldsymbol S)}{\boldsymbol E(\boldsymbol s)}Notas importantes:
- Si la función de transferencia H(s) de la trayectoria de realimentación (FT del sensor) es igual a uno, H(s)=1, sólo en este caso, la función de transferencia a lazo cerrado es igual a la función de transferencia de trayectoria directa;
- A la función de transferencia de trayectoria directa G(s) también se le conoce simplemente como Función de transferencia directa.
Aplicando álgebra de bloques a la Figura 1 podemos determinar la Función de Transferencia entre la señal de entrada R(s) y la señal de salida C(s) :
\frac{C(S)}{R(s)} = \frac{G(s)}{1 + G(s)H(s)}\ \ \ \ (3)A la función C(s) /R(s) de la ecuación (3) se le conoce como Función de transferencia en lazo cerrado (cociente entre la señal de salida y la señal de entrada)
Función de Transferencia en Lazo Cerrado: cociente entre la señal de salida C(s) y la señal de entrada R(s) :
\frac{\boldsymbol C(\boldsymbol S)}{\boldsymbol R(\boldsymbol s)} = \frac{\boldsymbol G(\boldsymbol s)}{1 + \boldsymbol G(\boldsymbol s)\boldsymbol H(\boldsymbol s)}La ecuación (3) nos permite obtener La Transformada de Laplace de la salida para cualquier entrada, una vez que sabemos cuál es la función de transferencia a lazo cerrado.
Te puede interesar:
- Se resuelven ejercicios de Señales y Sistemas, con carácter de Urgencia. EN MENOS DE 24 HORAS (precio aprox. por cada ejercicio (o cada pregunta): 13.7 euros)
- Clases Online: Si tienes alguna duda, Te Enseño este tema con paciencia y pedagogía. Podemos resolver ejercicios durante la clase (14.7 euros la hora)
- Contacto: Prof. Larry, Whatsapp: +34747458738, dademuch@gmail.com
- Otras áreas: Análisis Sistemas, Procesamiento de Señales, Simulación Matlab/Simulink, Sistemas de Control,
- Modelo y Análisis Matemático de Sistemas Eléctricos, Electrónicos, Mecánicos (MRA), Electromecánicos…
Este curso está en continuo crecimiento, trabajamos diariamente para publicar semanalmente más artículos. Al suscribirte podrás contar con excelente material para estudiar y superar con éxito las demandas académicas.
Curso relacionado:
Prof. Larry. Estudios:
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs